Prediction and design
Durandal
Although it is challenging to generate good models, to identify the best model among many generated by a stochastic method is also difficult. The simplest way is to select the lowest energy model. However, the lowest energy model is very often not the best model since there are errors in the empirical energy functions. Clustering methods are very often used to identify the best models based on the Boltzmann principle. However, it’s very time consuming to cluster a large set of models. Therefore, either a subset of low energy models are subjected to clustering or an approximation is made on the calculation of geometric distances between models.
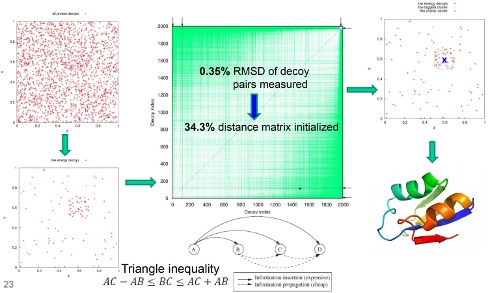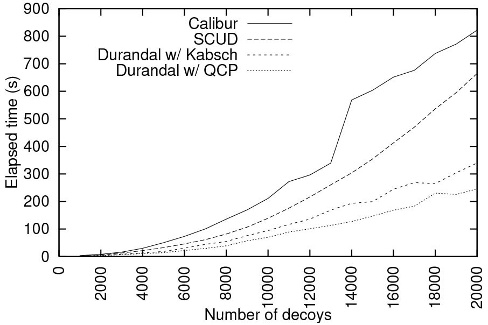
We proposed a method that calculates the distance matrix in an efficient manner. RMSD being a metric allows us to prune out computations taking advantage of the triangular inequality by measuring distances from all decoys to only a few reference ones. In the case of exact clustering, knowing only a range the distance will fall into is enough in many cases. This range can be narrowed down using only additions and subtractions, which is much faster than computing a RMSD. Our method is named Durandal. The figure below compares Durandal with a state-of-the-art exact clustering method, Calibur and an approximation method, SCUD. It shows that Durandal is not only significantly faster than Calibur but also faster than an approximation method, SCUD. In fact, Durandal was the fastest exact clustering method to the best of our knowledge.
This work has been published in Bioinformatics
(publication) and in the Journal of Computational Chemistry
(publication).
We proposed a method that calculates the distance matrix in an efficient manner. RMSD being a metric allows us to prune out computations taking advantage of the triangular inequality by measuring distances from all decoys to only a few reference ones. In the case of exact clustering, knowing only a range the distance will fall into is enough in many cases. This range can be narrowed down using only additions and subtractions, which is much faster than computing a RMSD. Our method is named Durandal. The figure below compares Durandal with a state-of-the-art exact clustering method, Calibur and an approximation method, SCUD. It shows that Durandal is not only significantly faster than Calibur but also faster than an approximation method, SCUD. In fact, Durandal was the fastest exact clustering method to the best of our knowledge.
This work has been published in Bioinformatics
(publication) and in the Journal of Computational Chemistry
(publication).