私たちのグループは、計算機や数理的手法を用いて、生命現象に取り組んでいます。特に多量の情報を統合して高次生命現象を理解する場合や、時空間中にパターンが展開する形態形成現象を理解するうえで、数理的手法は有効だと考えています。
現在の研究内容
制御ネットワークの構造とダイナミクス
生物の振る舞いが分子レベルで明らかにされて、様々な生体分子の活性の制御関係が、複雑なネットワークを構築していることが分かってきました。そのネットワークに基づくシステム全体のダイナミクスが、生命らしい振る舞いの起源なのだと考えられています。分子の静的な関係である制御ネットワークが分かってきたことにより、次の段階として生命システムのダイナミクスの解明が期待されています。しかし改めて考えてみると、制御ネットワークはダイナミクスを決定するための十分な情報をもちません。ネットワークは「どの分子がどの分子を活性しているか」という、依存関係の情報でしかないのです。ここからダイナミクスを議論するためには、微分方程式に含まれる関数の形やパラメータの値など多くのことを仮定しなくてはいけない、というのが通常の数理モデルの考え方でした。
これに対し、我々は発想を変えて解決に臨みました。「システムに含まれる分子の依存関係」の情報しか得られないのであれば、「それだけから決められるダイナミクスの性質」を議論できないか。この発想に基づき、ネットワークの構造とダイナミクスとを直接・仮定なしに結び付ける、Linkage logicが完成しました。Linkage logicにより、以下の事柄が保証されます:
- システムから作り出されるあらゆるダイナミクスは、ネットワークに含まれる一部の分子の振る舞いで捉えられます。
- またそれらの分子は制御ネットワークの構造だけから決定できます。
- またこれらの分子は、システムのダイナミクスを操作するために十分な分子でも有ります。
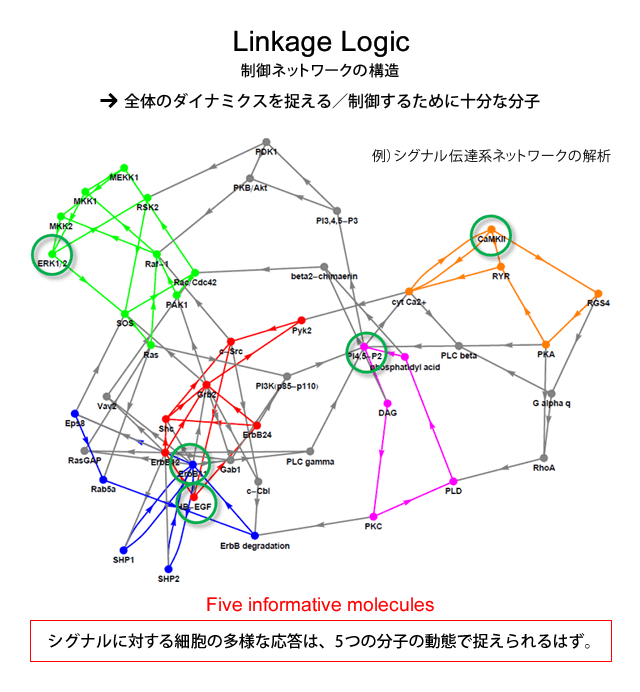
例えばシグナル伝達系は、細胞外のシグナル分子を受け取って、細胞が様々な可能性の中から行動を決定する回路として知られており、100以上の分子からなります。既知のネットワークは複雑そうに見えますが、解析によりこのダイナミクスはたった5つの分子の動態で捉えられるはずだと分かります。つまりネットワークが正しければ、ありとあらゆる細胞応答は5つの分子のダイナミクスに帰着できるはずです。
我々はこの理論の次の展開として、実験グループとの共同研究による理論の検証や、実験と理論を組み合わせることによる、生命システムのダイナミクスのより深い理解を目指していきます。