私たちのグループは、計算機や数理的手法を用いて、生命現象に取り組んでいます。特に多量の情報を統合して高次生命現象を理解する場合や、時空間中にパターンが展開する形態形成現象を理解するうえで、数理的手法は有効だと考えています。
現在の研究内容
細胞内膜構造の物理的理解
私たちの細胞(真核細胞)には、たくさんの膜でできた構造物"オルガネラ(細胞小器官)"があります。膜タンパク質や分泌タンパク質を加工(修飾)し必要とされる場所への配送を仕分けするゴルジ体や酸素と代謝物質からエネルギーを取り出すミトコンドリア、栄養飢餓状態で現れ細胞内物質を分解して細胞の材料を供給するオートファゴソームなど、これらオルガネラはそれそれが固有の機能を担い、互いに連携しあう事によって細胞内部での分業を促進させ、細菌などの原核細胞には見られない複雑な機能や多様な外部との係わりを可能にしています。オルガネラの働きは、真核細胞を理解する上で欠かすことのできないプロセスです。
オルガネラは細胞膜と同じ脂質二重膜からなるさまざまな形(構造)を持った物体です。この形の多様さもオルガネラの魅力の一つで、さらに形はその機能と密接に関わることから、形の成り立ちを理解することはオルガネラを理解する上で重要な意味を持ちます。さて、細胞は一般にとても小さく(~10μm)、その部分である膜構造物はさらに小さいものです(~100nm)が、その形の成り立ち、振る舞いはどのように調べることができるでしょうか?形そのものは電子顕微鏡で観察できます。しかし、電子顕微鏡で細胞を観察するためには細胞を凍結させたり薬品を使って固定する必要があるため、オルガネラを含む細胞の内側が動いている様を直接見ることはできません。オルガネラの成り立ちや振る舞いを理解するためには、固定した細胞の観察"スナップショット"から、実際に何がどういう順番でおきているか、ダイナミクスを推測することが必要となります。
我々はこの問題に対し物理モデリングとコンピューターシミュレーションを用いることによって、誰も見たことのないオルガネラのダイナミクスを再現し、その成り立ちや振る舞いを理解すること目指しています。

物理学で物体の運動はその物体の持つエネルギーを求めて解きます。膜は曲がった部分にバネのように弾性エネルギー(Helfrichの自由エネルギー)を蓄えるため、膜の形から直接エネルギーを計算し、変形運動を解くことができます。オルガネラのような複雑な形態は膜を曲げる分子が多数介在することにより実現されますが、それら分子の寄与は弾性エネルギーの変化として記述し、生体膜のベーシックな物理モデルを作成しました。このベーシックなモデルを元に各オルガネラに特異な膜変形分子の性質を付与すれば、各オルガネラの物理モデルとなります。
しかし、ここで問題があります。それはどのオルガネラにどのような性質の膜変形分子が存在するかほとんど分かっていないことです。そのかわり我々が得られるのは、前述の形態の"スナップショット"です。そこで我々は、ベーシックなモデルと形態の情報から膜変形分子の性質を推定しつつオルガネラのモデルを作成し、そのダイナミクスを解くという方法で研究を進めています。現在我々は
- ゴルジ体の再集合過程のモデリング
- カベオラの浸透圧ショックに対する応答
- オートファゴソーム形成を可能にする膜変形分子
の各テーマについて解析を進めています。
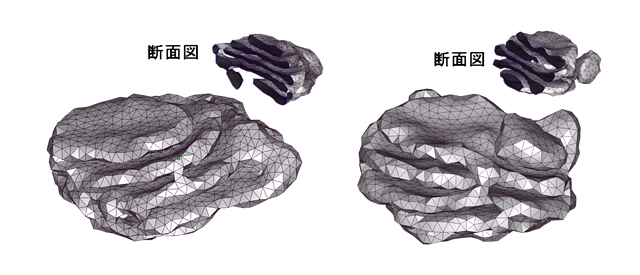
ゴルジ体再集合モデルのコンピューターシミュレーション
ポリゴンで表現した膜形態モデルを用いモンテカルロ法で変形ダイナミクスを計算することで、細胞分裂におけるゴルジ体再集合の過程をコンピューター内に再構成し、その物理的な性質をさぐる。
