Click here for Abstract in English
written by M. Tamura (December 2002)
[Pd(dmit)2]という金属錯体分子がつくる結晶の磁化率を調べたところ,これまで実例がほとんど知られていなかったスピン-1/2ハイゼンベルク二次元三角格子反強磁性モデルの特徴が明確に現れていることが初めてわかりました.このモデルは,磁気的フラストレーションという現象を示すもっとも基本的なもので,これが分子性結晶において発見されたことは意義深いことと考えています.
この研究結果は,英国で出版されている学術誌 Journal of Physics: Condensed Matter の第14巻47号L729-L734 ページに掲載されました(2002年11月). 同誌の電子ジャーナルサービス により誰でも無料で閲覧できます.
ここではその背景や意義について,若干の独断を交えつつ,ややじっくり,なるべく式は省略しながら,ところどころ詳しく書いています.1人の分子磁性体研究者の「つぶやき」も混じります.結果だけ書いても論文と同じになってつまらないので,よけいなことをたくさん書きました.手っ取り早く結果を知りたい方は,最初の方を適当に読み飛ばしてください.
またごく最近,京都大学理学部と東京大学工学部の共同研究で,やはり有機分子からなるκ-(BEDT-TTF)2Cu2(CN)3という物質で,フラストレーションの顕著な効果が見つかってきました.我々はその結果にも注目しています.

物質の磁性は,その中の分子(やイオン)にある電子が磁石としての性質をもっていることに由来します.電子の磁石の向き(N極の向き)はスピンと呼ばれます.分子の中でほとんどの電子は,スピンが逆向きの2個ずつでペア(このペア1つが共有結合1本になる)になって互いに打ち消し合うため,磁石としての性質が消えてしまいます.分子の種類によっては結合に参加せずに余っている電子(不対電子)をもつものがあり,そのような分子は,打ち消されていない電子のスピンを背負っているので,ミクロな磁石としてふるまいます.磁性体とはそういう分子がつくる物質のことで,その構成分子のもつ電子のスピンがどのように配向するかによっていろいろな種類があり,それぞれ特徴のある磁性を示します.
もっとも目立つ磁性体は強磁性体です.その中ではすべての分子のスピンが同じ向きにそろっているので,物質全体が磁石の性質を示し,ほかの磁石に引き寄せられたり,磁場がかかっている方向に向こうとしたりします.これは隣り合う分子の間でスピンを同じ向きにしようとする力が働いている(平行になった方がエネルギーが下がる)結果として,多数の分子の協同作業として物質全体の性質が決まっているわけです.
逆に,隣り合う分子の間でスピンを逆向きにしようとする力が働いている(反平行になればエネルギーが下がる)物質もあります.これは反強磁性体と呼ばれます.外部から見ると磁性が消えているように見えますが,この場合も多数の分子の協同作業として全体の性質が決まっています.多くの場合,スピン間に働く力は,(相対的な)向きを互いに同じにするものか逆向きにするものかのどちらかです.中途半端な向きに向ける力はないか,あっても非常に弱いものです.
温度が高くて熱エネルギー(磁性体の場合はスピンの向きをランダムにしようとする)が分子間でスピンを整列させる力(相互作用)に勝ってしまえば,協同作業が成り立たず,全体としては磁性が消えてしまいます.これを常磁性と呼びます.鉄の磁石も高温に熱すれば常磁性になり,磁石ではなくなります.しかし分子間相互作用が存在すれば,ところどころ確率的にその影響が残るので,低温に向かってスピンが整列しようとしている傾向が実験データから読みとれます.

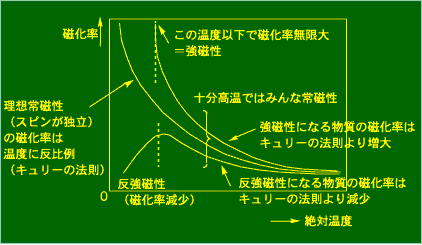
磁性にはそのほかにも百科事典ができるほど多数の種類がありますが,ここではこの3種類にしておきましょう.
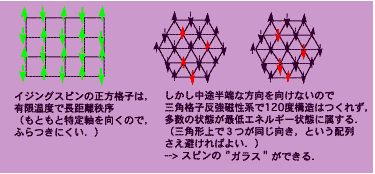
反強磁性の場合を考えます.まず少数個の磁石からなる小さな系で,磁石が2個の場合や四角形の頂点上に4個ある場合では,図のように配向したものが最も安定な状態です.4個を放射状においても同じように考えればすみます.隣接磁石を逆向きにすればよいだけのことです.
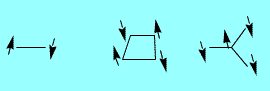
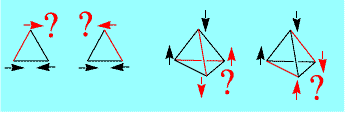
しかし,次の図のように,三角形の頂点上に3個ある場合,四面体の頂点上に4個ある場合などには,うまくいきません.どこかで2つが同じ向きになってしまいます.これが磁気的フラストレーションで,あちらをたてればこちらが立たず,欲求不満がたまってしまう状況です.頂点のつながり方に三角形が含まれていて,三者間の関係を同時に逆向きという形で満足させられないわけです.
多数の分子磁石を含む固体でも同じようなことが起きます.結晶格子上に並んでいる分子に,スピンの向きを,↑と↑,や,↓と↓,が隣り合わないように割り当てることができれば,いいかえると,どの隣接分子間でもスピンが逆向きになるようにできれば,それが最も安定な状態です.(食塩の結晶でNa+イオンとCl-イオンに格子点を割り振るのと同じです.)絶対零度ではこの状態になります.
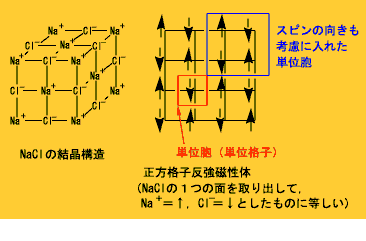
ところが,こういう割り当てができない結晶格子もあります.その最も簡単で代表的な例が三角格子です.三角格子のように,分子(格子点)をつないでいくと三角形ができる場合,隣接分子のスピンの向きをすべて逆向きにするのは不可能です.反強磁性体では,ある隣接スピンのペアが逆向きなら,そこのエネルギーが下がって満足するわけですが,三角形ができていると,3つを同時にすべて互いに反平行にすることができず,何らかの妥協が強いられます.欲求不満が残ってしまう,というわけで,この状況をフラストレーションと呼んでいます.
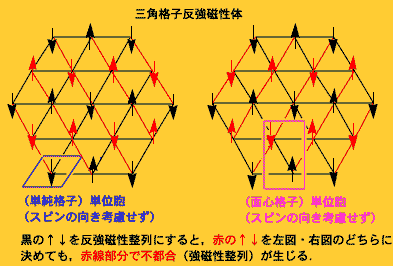
人間世界でも,三者間の関係となると途端に話がややこしくなることがありますね.三すくみ,三角関係,三つどもえ,人が三人寄れば政治が始まる.....物理でもそういうことが起きるのです.じゃんけんの原理はここにあります.これが強磁性体の場合なら,三位一体,三国同盟,三本の矢(毛利元就),で特に問題は起きないのですが.
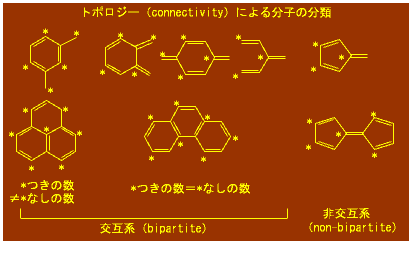
単なる反強磁性ですむか,それともフラストレーションなど特殊な事情を考慮せねばならないか,を分ける1つの基準は,配列がbipartiteであるかないかです.(bipartiteは二分割性とでも訳せばよいかと思います.これは磁性物理学での用語で,量子化学ではこれとは別に古くから交互系・非交互系という分類が,ほとんど同じ意味で用いられています.)格子点上のある点に*印をつけ,その隣接点は*印なしとする.以下,*なしの隣は*つき,*つきの隣は*なし,と割り振っていって,格子全体を*つきと*なしに矛盾なく(*つきどうしや,*なしどうしが隣接しないように)分割できればbipartite(交互系)です.すぐにわかりますが,格子が奇数角形を含まなければbipartiteです.
この種の構造の分類のことを,数学ではグラフ理論,物理では connectivity(連結性),化学ではトポロジーと呼んでいます.交互系の理論を適用すれば,分子の基底状態の磁性に関して面白いことがわかるのですが,その話にはここでは立ち入りません.
三角格子反強磁性体がどんな状態でエネルギー最低になるかは,分子のスピンがどんな性質をもつかで大きく変わると考えられています.それによって妥協の仕方が変わってくるからです.
まず分子のスピンが,ふつうの磁石と同じように,決まった向きをもつが状況に応じてその向きは自由に変えられるものだとします.(これを古典ハイゼンベルクスピンと呼んでいます.)この場合,隣接分子のスピンが互いに120度の角度をもつようになれば,全体のエネルギーが最も低くなることが知られています.隣接で逆向き(180度)だとそのペアのエネルギーは最低になるのですが,そうするとほかのスピンとの間で不利になってしまうので,すべてを120度にすることで妥協してしまうわけです.この予想に対応する実験結果も存在します.

ところが,ミクロな分子の磁石は,量子力学というミクロ世界の物理法則のせいで,本当はふつうの磁石と違った奇妙な性質を示します.分子に乗っている電子のスピン(量子ハイゼンベルクスピン)は,ある特定方向に完全に向いてしまうことはなく,倒れかけたコマのように,ある方向を中心に絶えずふらついています.もう1つ,2個の電子は区別ということを受け付けない(どっちがどっちなのか印がつけられない)という性質もあります.2個の電子スピンの間に逆向きにする力が働けば,こうした性質の結果,共鳴という現象が起きます.互いに相手と逆向きになるだけでなく,相手が下の方を向けば自分は上の方を向き,相手が上の方を向けば自分は下の方を向く,ということを絶えず繰り返して,2個の電子のスピンは渾然一体となった状態をつくります.実は,水・砂糖・アルコールなどふつうの分子の中では,すべての電子が2個ずつ組合わさってこの状態になっていて,磁石としての性質が決して表に出てこないようになっています.

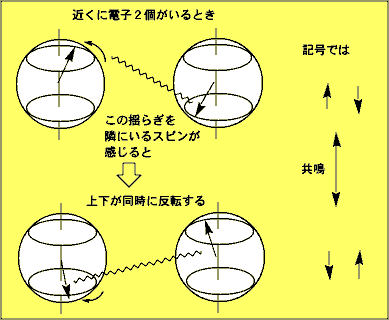

では電子3個ならどうなるでしょうか?3個のうち2個の電子が結びつけば1個あぶれます.しかしどの電子も自分が差別されるのを嫌がるので,さらに共鳴が起きて,結びつく相手をどんどん入れ替えてしまいます.この状態を化学者は図のように表します.どの頂点上にも1/3に縮まったスピンがあるように見えます.正三角形1つだけ(分子3つだけ)なら,これが解答です.
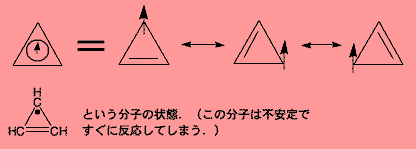
なお,この三角形の一辺だけ切断すると,まんなかのスピンが逆向きになるということも起こります.実はこれは有機強磁性体の分子の状態を論じる基本であるスピン分極という現象ですが,ここでこれ以上は触れません.

結晶格子として,無数の三角形が連なっている三角格子では最低エネルギーの状態はどうなるでしょうか?実はこれはまだ完全には決着がついていない大変難しい問題です.量子力学の効果でうんと縮まったスピンが,隣接では互いに120度に傾いて整列している,というのが大方の予想のようですが,本当のところは誰も知りません.さらに,この基本問題に近似的にでも当てはまる物質の実例というのもほとんど知られておらず,実験でこの問題に迫るのも難しい状況でした.
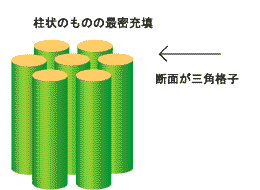
三角格子のような分子配列は決して特殊なものではありません.コインや団子のような丸いものを平面上に敷き詰めれば(最密充填)自然にそうなります.もちろん分子はまんまるではないので,実際には大なり小なりいびつになります.

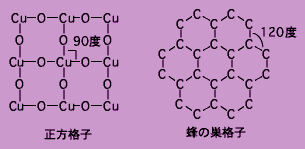
また,分子でも原子でも,スピンをもつものは隣のものと結合をつくろうとする傾向があり,結合というものは互いに120度(π結合に関係して現れやすい)や90度(遷移金属のd軌道がかかわる場合に多い)などの角度を保とうとする性質があるので,蜂の巣型格子や正方格子などができることも多くなります.(三次元ではさらにダイアモンド格子や立方格子などができます.)平面内で三角格子のように60度の角度で6本の強い結合をつくるのは困難です.しかし結合があまり強くなければ,方向性よりも分子の充填の方が優先されるので,三角格子ができる可能性があります.三次元でも面心立方格子や六方最密格子はbipartiteではなく,フラストレーションが関わってきます.
なお,イオンや原子が直線的につながった柱状のものが束になるときに三角格子が形成される場合もあります.この例は無機系化合物でたくさんあり,柱と柱の間で反強磁性的相互作用が働けばやはりフラストレーションを起こしますが,柱の中にすでにたくさんのスピンが含まれているので,平面内の三角格子とはやや違った趣の問題になります.
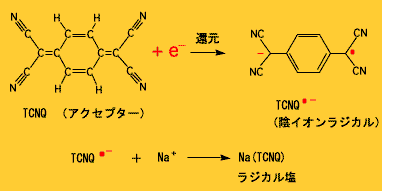
ここで登場するのが,有機分子のつくるラジカル塩という物質群です.有機分子でπ電子をもつものには,比較的酸化されやすい(電子を奪われて陽イオンになりやすい)ドナーと呼ばれるものがあります.逆に,比較的還元されやすい(電子を与えられて陰イオンになりやすい)アクセプターと呼ばれるものもあります.このような分子を酸化して電子を1個除く(または還元して電子を1個与える)と,不対電子をもつようになります.不対電子をもつ分子をラジカルと呼びますが,今の場合には電荷ももっているので,特に陽イオンラジカル,陰イオンラジカルと呼びます.
ラジカルという語は,過激な,という意味ももちますが,ここでのラジカルは,根源的な,という意味です.不対電子をもつ原子団は,同じように不対電子をもつ原子団と結合してもっと複雑な分子をつくる根源的要素であると見なされます.分子を部分に分けたものを○○基と呼ぶときの○○基がラジカルです.
このようなイオンラジカルは,逆の電荷をもつイオン(Na+とかCl-のようなふつうのイオンでもよい)と一緒になって塩になります.これがラジカル塩です.ラジカルは不対電子をもっているので,少なくとも分子単独ではミクロ磁石の性質を示すはずです.同時に,イオンラジカルは電荷をもっており,お互いに反発する傾向があるので,ラジカルどうしで強い結合をつくって不対電子を完全に失うことはあまり起きません.また,複数の不対電子をもつことが多い遷移金属イオンの化合物に比べて,ほとんどの有機分子ラジカルは不対電子を1個だけもつので,量子力学的に見ると,より基本的なスピン系を提供します.(有機分子を使った方が,見かけの構造の複雑さに反して,純粋な電子スピンの磁性が観測される,ということ.)

実はラジカル塩は,有機伝導体や有機超伝導体を与える最も重要な物質群です.2000年のノーベル化学賞を受賞した白川先生の電気伝導性高分子(ポリアセチレン)も,ヨウ素で酸化されて分子の一部が陽イオンラジカルに変わることで,電気伝導性を発揮します.また今回我々が研究した化合物も,数千気圧の圧力をかければ電気伝導性になります.電気伝導性や超伝導の詳しい話は,別の機会に譲ります.
ラジカル塩は,NaClのようなものとは違い,陽イオンと陰イオンの大きさや形が非常に違っていることが多いので,それらが別々の層をつくり,それがサンドウィッチのように交互に積み重なった層状構造をしばしばとります.また組成も1:1以外に,2:1や3:2といったやや複雑なものになりやすい傾向があります.ラジカルイオンの層内では,分子どうしがごく弱く結合しながら(分子内のふつうの結合の1/10程度以下の強さ)なるべく余分な隙間をつくらないように充填されています.こういう事情で,ドナーやアクセプターのラジカル塩では,三角格子に近い構造ができやすい条件が潜在的に存在しています.
実際,有機結晶には三角格子のように見える分子配列がしばしば現れます.もちろん三角格子型の配列だけでどんな分子でも磁気的フラストレーションが働くわけではなく,各格子点にスピンをもった分子が存在しなければなりません.また前述のように,ごく一部の例外を除いて有機分子のつくる充填構造は理想的な三角格子からずれて多少はいびつになっています.フラストレーションの働く三角格子が本当に実現しているかどうかは,実験できちんと確かめる必要があります.(分子間でスピン間に働く力は,結晶構造がわかっていれば,分子軌道間の重なり積分から推定することができます.しかし,重なり積分の数値的絶対精度は期待しない方がよいでしょう.重なり積分による固体物性の推定は,大きさのオーダーがどの程度か見積もるとか,同系統の物質間で相対的な序列をつけるなど,定性的な範囲にとどめておくのが健全だと思います.)
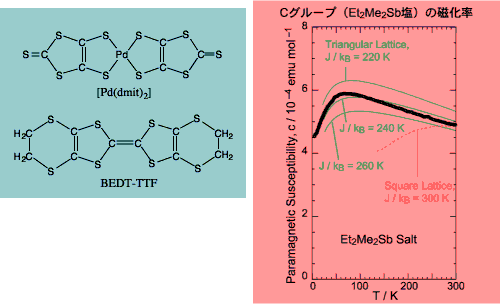
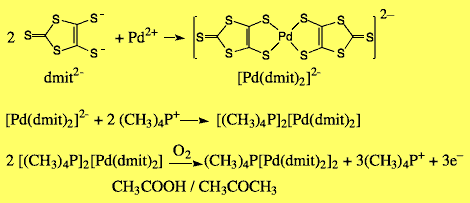
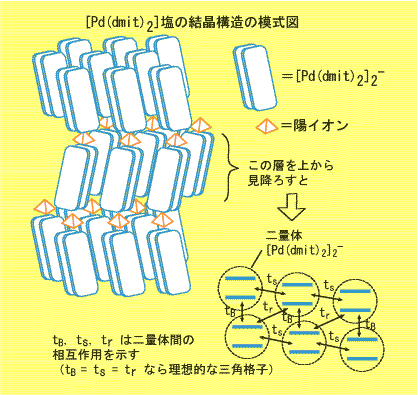
この分子は 1980 年代後半から研究されてきたものです.合成直後の dmit は−2価の陰イオンで,その溶液に Pd2+ の塩を加えることにより, [Pd(dmit)2]2- の塩がまず得られます.その酸性溶液を空気酸化することにより, [Pd(dmit)2]- を経て, [Pd(dmit)2] 0.5- という平均価数をもつ単結晶が得られます.この結晶は [Pd(dmit)2] と+1価の陽イオンとの 2:1 の組成の塩で,結晶中で [Pd(dmit)2] は2個ずつ強く結合して二量体になっており,その二量体1個に不対電子1個が入って陰イオンラジカルとなっています.この陰イオンラジカルは [Pd(dmit)2]2- と表すのが適切です. [Pd(dmit)2] 塩では,この [Pd(dmit)2]2- が三角格子のように配列して層をつくり,陽イオンの層と交互に積み重なっています.
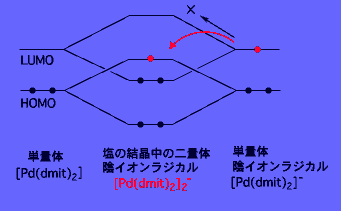
あとの磁性の話に直接の関係はありませんが,この [Pd(dmit)2]2- ではちょっと珍しいことが起きています.陰イオンラジカル [Pd(dmit)2]2 - の状態で実際に不対電子が入っている軌道は,単量体の [Pd(dmit)2] がアクセプターとして電子を受けとって収容する軌道( [Pd(dmit)2] の最低空軌道 LUMO )とは別の軌道になっています.このようなことが起きるのは,二量化が非常に強くて, [Pd(dmit)2] の LUMO とその下の準位(最高占有軌道 HOMO )がそれぞれ大きく二分裂するので,元の HOMO から上昇した準位が LUMO から下降した準位を上回り,二量体になったときそちらが LUMO としての働きをもつことによります.(二量体 [Pd(dmit)2]2 の LUMO は単量体 [Pd(dmit)2] の HOMO 由来ということ) Pd ではなく Ni を使った場合にはこのようなことは起きません.以上のことは 1990 年前後に計算と光スペクトルの実験から証明されました.
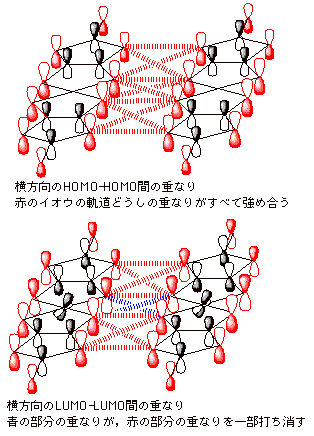
陰イオンラジカル [Pd(dmit)2]2- で不対電子が入っている軌道が 単量体の HOMO 由来であることは,層内で分子間に二次元的な相互作用ネットワーク(一次元的なものではなく)が形成されるのに有利に働きます.単量体の HOMO は分子の縁の硫黄原子が同符号の軌道係数をもちますが, LUMO では分子の半分で反対符号になります.隣接分子の縁どうしが接触して結合をつくるとき,同符号であれば軌道間の重なりが増強されやすくなり,分子間相互作用が相対的に強くなります.
[Pd(dmit)2]2-のもつ不対電子が二量体間で自由に動き回れれば,二次元金属伝導状態が実現されます.(数千気圧の圧力下では実際にその状態になって電気伝導性があると考えられます.)しかし,1単位あたり1個の不対電子がある場合には,自由に動けなくなる事情があります.すべての単位に1個ずつ不対電子がある状態から,不対電子1個を別の場所に動かすと,不対電子が2個ある場所ができてしまいます.このような場所では,不対電子どうしの反発力が強く働き,エネルギーの損失が発生します.それを避けるために,不対電子は動かずにそれぞれの場所にとどまろうとします.この状態をモット絶縁体と呼びます.モット絶縁体のように電子間の反発力によって電子の状態が強く影響されているものを強相関電子系と呼んでいます.高温超伝導も強相関電子系で起きる現象であると考えられていて,強相関電子系の物理学は非常に盛んに研究されています.
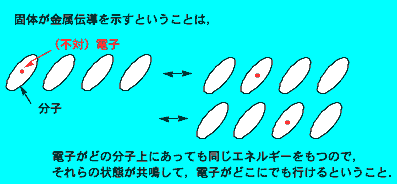
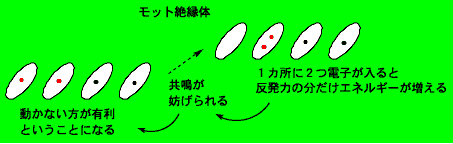
もし1単位あたりの不対電子数が1からずれていれば,もともと不対電子が2個またはゼロの場所が存在します.そのような場所を動かしても,同じ場所に不対電子が2個はち合わせすることによるエネルギーの損は新たには発生しないので,結果として不対電子は自由に動けて,金属伝導状態になります.(しかし,背景にモット絶縁体の性質が見え隠れします.)
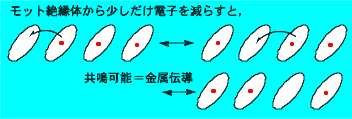
1単位あたりの不対電子数が1でも,同じ場所にある2個の不対電子間の反発力がたいしたことがなければ,不対電子が動き回ることでいろいろな状態が共鳴した方がエネルギーの得があるので,金属伝導が現れます.分子間の結合が強くなればこのエネルギーの得が大きくなるので,モット絶縁体に圧力をかけて分子間を接近させることによって金属伝導が現れることがよく見られます.
圧力をかけなければ [Pd(dmit)2] 塩はモット絶縁体です.モット絶縁体では不対電子は動き回れず,できることはスピンの向きを変えることだけです.つまり磁性体としてふるまいます.(モット絶縁体ではないふつうの絶縁体では,そもそも不対電子も存在しません.したがって磁性体でもありません.)
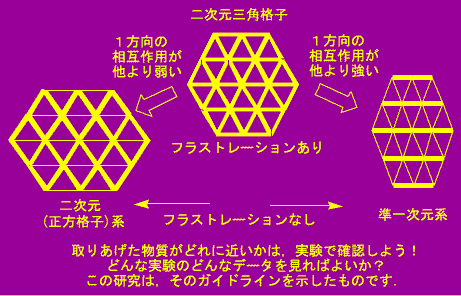
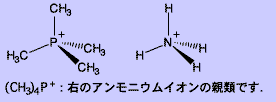
1990年代に,似た形の陽イオン((CH3)4P+,(CH3)4As+,(CH3)4Sb+,(CH3)2(C2H5)2P+, (CH3)2(C2H5)2Sb+ など)と[Pd(dmit)2]の塩が相次いでつくられ,基本的には同形で少しずつ異なる構造をもつ一連の結晶が研究されて,シリーズの中での微妙な違いを相互比較できるようになりました.共通の構造パターンは図に示したとおりです.圧力をかけなければ,どれも同じような絶縁体です.しかし圧力をかけたときの電気伝導性には違いが出てきます.
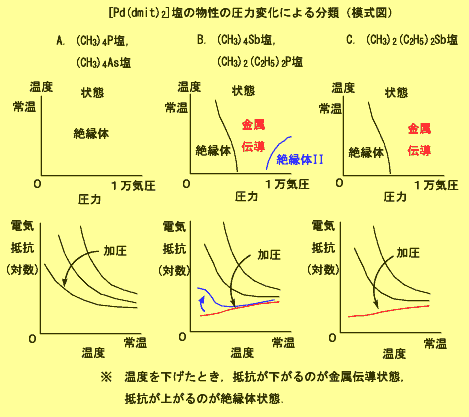
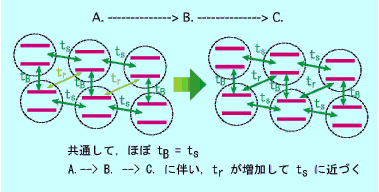
なぜこのような違いが出てくるのか,X線実験で決めた結晶構造に基づいて,分子配列の違いが調べられました.その結果,A.の塩では,1つの二量体から3方向に延びる相互作用のうち1つがやや弱く,B.を経てC.になると,3つがほぼ同じ強さになることが推定されました.つまり,A.-> B. -> C. の違いは,だんだん三角格子に接近し,フラストレーションが強くなることによるのではないか,という仮説が提案されました.(S. Rouziere et al.: Phys. Rev. B 60 (1999) 3113.)
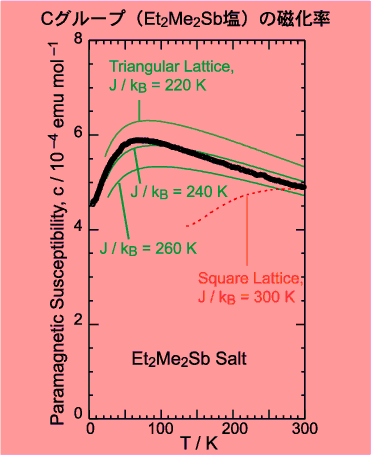
次に,電子スピン共鳴(ESR)という実験で一連の塩の磁気的性質も調べられました.(T.Nakamura et al.: J. Mater. Chem. 11 (2001) 2159; Mol. Cryst. Liq. Cryst. 379 (2002) 53.) その結果,A.やB.の塩は,ある温度(ネール温度)以下で,スピンが反強磁性配列していることがわかりました.ネール温度はA.ではB.の約2倍で,約40 Kです.ネール温度が高いほど反強磁性配列が実現しやすいといえます.フラストレーションが強ければそれだけ反強磁性配列がじゃまされて起きにくくなるはずですから,ネール温度は低くなるはずです.フラストレーションが最も強いと思われた(CH3)2(C2H5)2Sb塩では,ネール温度は低すぎて見つかっていません.
このように [Pd(dmit)2] 塩では,圧力下での電気伝導と結晶構造や磁気的性質の相互比較から,三角格子系としてのフラストレーションの役割がクローズアップされてきました.となると,反強磁性配列が起きる温度より上の常磁性状態で,実際にフラストレーションが働いているという実験的証拠がますます必要になってきます.
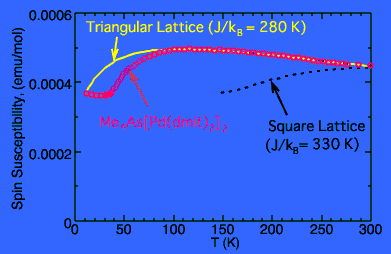
以前から[Pd(dmit)2]塩の磁化率測定結果の報告はいくつかありました.すべて似通っていて,室温から温度を下げていくにしたがって徐々に上昇したあと,70-100K程度でまるいピークを示して絶対零度に向かってやや下がるという傾向を示します.しかしその値や温度依存性の意味については何も議論されていませんでした.磁化率そのものの値が小さく,顕著な温度変化もなく,こういった特徴をきれいに説明するようなポピュラーなモデルも知られていないためでしょう.
今回の研究では,(CH3)4P塩と(CH3)2(C2H5)2P塩のデータは以前からあるものを使い,新たに(CH3)4As塩,(CH3)4Sb塩と(CH3)2(C2H5)2Sb塩の測定をおこなって,これら5種類を比較してみることにしました.実をいうと,最初は(CH3)4As塩の磁化率を測定して反強磁性整列する温度などを確かめて,ほかのデータとあわせて1つの論文にまとめるつもりで実験を始めました.(CH3)4As塩の試料は特に質のよいものを選んで使ったので,補正のためのデータ処理をしないでも,これまででいちばんはっきりと反強磁性整列が測定されました.しかし筆者が自分で測定したデータを扱っているうちに,温度変化全体に筋の通った説明をつけたくなり,いろいろ考えたり調べたりしているうち,このデータがフラストレーションの効果の明白な証拠になっていることに気づきました.
ここまでの背景説明では,磁気的フラストレーションを実験で確かめるべく研究を進めていたように書いてきましたが,それは後知恵というもので,本当はそうではなく,筆者自身はフラストレーションの役割についてはどちらかといえば懐疑的だったのです.いよいよ自分の実験データを目前にしてみると,フラストレーションの効果は否定できなくなり,そこにそれが現れているという結論に自然に導かれました.というわけですから,この結論は十分に信用してもらってもよい,と思っています.
世の中には,結論を予め用意した研究なんていうものもあり,はなはだしい場合には研究費目当てにデータを捏造するということさえあると聞き及びます,そこまでいかなくても,都合の悪いデータを無視してしまったり,データから結論に至る間の論理を飛躍させて無理な結論を主張したり,といった例は少なくありません.データそのものが情報不足でいろいろな解釈を許す場合に結論が分かれるのはしかたありませんが,明白な動かしがたい事実に出会っているのに結論をこじつけると,それを見破れるごく少数の専門家はともかく,それ以外の人々も混乱させます.研究の目的指向化が行きすぎて,特定目的を達成するための競争が過剰になると,こういう弊害が増えてくるのではないかと心配になります.
話がだいぶそれてしまいました.(そらしたのは筆者ですが.)まだ誰もつけていない磁化率の説明をやってみようと,まずフラストレーションのない一次元系や二次元系(正方格子)の理論式とデータを比較してみました.これらのケースではよく知られた理論式があって,試してみるのは簡単です.すぐに,こんなケースとはデータが合わないことに気づきました.理論式の値を約半分にして定数を加えるなどとすれば不思議に合ってきましたが,そんな意味不明の値を掛けたり足したりするのはひどいこじつけというものです.
そこで自分が前から知っている式でデータを説明するのはあきらめ,三角格子の可能性を念頭に置いて,これまでにそういう観点から研究された物質の実例を捜してみました.もしぴったりの類似品があれば,その研究を引用して自分のもそうだ,と書けば簡単に論文が書けます.(楽ですがつまらないですね.)しかしなかなか見つかりません.明らかに誤っているのもありましたが,スピン以外の効果が出てきたり,温度を下げると相転移を起こして別の型のシステムに変わったりした惜しいものもありました.どうやら,電子1個分のスピン(スピン1/2といいます.電子2個分ならスピン1です.スピン1以上の二次元三角格子の実例は比較的豊富にあります.)が二次元三角格子になっているという確信のもてる実例は,これまでほとんど知られていないようです.捜しているうちに,1993年に書かれたスピン1/2二次元三角格子の磁化率を理論計算している論文(N. Elstner et al.: Phys. Rev. Lett. 71 (1993) 1629.)が見つかりました.その論文に出ているグラフを見て,これは自分のデータによく似ている,とすぐに思いました.
その論文は実験データとの比較についてはわずかしか言及していません.やはり実例が知られていないからでしょう.論文自体は,スピン1/2二次元三角格子の最低エネルギー状態(絶対零度の状態)について手がかりを得る目的で,温度の高い状態から逐次的に低温まで物性量の変化を求める高温展開という計算を高精度で実行した結果を報告したものです.論文の結果を実験データと比較するには,パデ近似子による外挿計算をさらにおこなう必要がありました.この手法は,高温展開の多項式がある次数で打ち切られていることによって生じる数学的にまずい挙動(磁化率が発散したりゼロや負になったりする)を避けて低温まで正確なようすを求めるために,多項式を有理式で置き換える,というものです.その論文で磁化率の温度変化をグラフにするのにも使われています.
たとえば, 1 - x + x2 - x3+ x4 - ... という級数が与えられたとします.これは,|x| がゼロから増えて1に近づくとなかなか収束しなくなり,|x| が1以上では収束しません.途中で打ち切ったことによる誤差も評価不能です.(x = 1のとき,1 - 1 + 1 - 1 + ... = (1-1) + (1-1) + ... = 0,とやってはダメですよ.)しかし有理式による表現を使うと,1- x + x2 - x3 + x4 - ... は実は (x+1)-1を表していることがわかります.これがパデ近似子の考え方です.(x+1)-1なら,マイナス1以外すべてのxで正確に値が求められます.多項式で展開したときは,どこかに発散する点があれば,展開の中心からその点への距離を半径とする円(収束円;複素平面内での話です)の内部でだけ展開が収束するという性質があります.そのため,x = -1と関係がないように見える x = 1 のところでも1 - x + x2 - x3 +...は収束しなくなります.一方,発散が起きる特異点を除いて無限回微分可能で,ある領域で完全に一致する2つの関数については,その2つの関数は同じものを表していて,定義域の広い方で全体をカバーできる解析接続という方法が適用できます.今の場合は,(x+1)-1が,原点の周り半径1の円内で1 - x + x2 - x3 +...と一致していることを利用して,円の外側にも解析接続(延長)したわけです.一般のパデ近似子の応用では,(x+1)-1にあたる関数が未知で,ある次数までの多項式展開しかわかっていない場合に,多項式展開の数学的制約をはずして最大限の情報を引き出す手法,と理解しておけばよいでしょう.
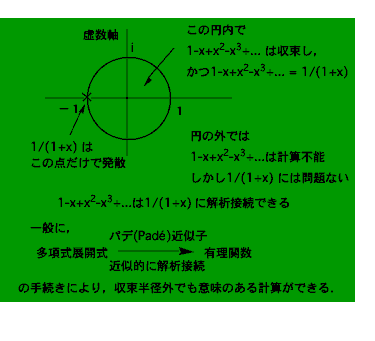

パデ近似子は多くの数理解析で使われますが,特に相転移温度付近の物性量の挙動を解析するのには古くから用いられているので,磁性体の統計力学を学んだ人にはよく知られています.実際,一次元や二次元のフラストレーションのない系の理論式は,類似の手法でつくられたものが以前から使われていたわけです.パデ近似子を作るのは,多項式=有理式,とおいて分母を払い,各次の係数を一致させるように,連立方程式を解くだけのことです.さっそくやってみると,論文に描かれているのと同じ理論計算のグラフができました.直接に実験データと比較できる有理式表現を与えた論文がないのは,そういうデータを抱えて必要に迫られた人がいなかったからでしょう.そこで今度は,理論計算のグラフと実験データのプロットを比較すると,驚くほど似ていました.この瞬間,筆者はフラストレーションの効果がデータに現れていることを確信しました.と同時に,極低温に冷却したり,複雑な測定をおこなったりしなくても,磁化率測定というおなじみの実験でフラストレーションの効果が見えたことについて,ある種の安心とあっけなさを感じてしまいました.
考えてみればこれは自然なことです.二次元三角格子上のスピン1/2量子ハイゼンベルク反強磁性系,というのは,あくまで理想化した理論モデルであって,現実の物質では,正三角形からのずれ,層間の弱い相互作用(非二次元性),磁気異方性(ハイゼンベルグスピンからのずれ),不純物の効果,試料の形状の効果など,モデルからの小さなずれが必ずあります.小さなずれは,その効果が熱エネルギーに打ち消されないような低温になれば無視できなくなります.逆にいえば,重要なものから順に高温から現れてくるということです.だからまず温度の高い領域のデータをよく説明するモデルを捜せば,それが対象の重要な特徴を拾い出したことになります.(逆にいえば,ある理論モデルで磁化率実験データの低温部だけ説明できても,高温部がまるで不一致なら,何か根本的な間違いを犯していることを疑うべき.)とはいえ,高すぎる温度では,あまりに自明な(重要すぎて,当たり前の)こと---たとえば,スピンが存在するとか,何か反強磁性的な相互作用が働いているとか---しかわかりません.今の場合では,磁化率の丸いピークに達したあたりで,この物質群全体のもっとも重要な特徴を拾ったことになります.もっと低温に行くと,反強磁性整列が見られる物質が出てきますが,これは物質群の中での差異を表す第二の特徴です.もっとよく調べようとしてさらに低温に行けば,モデルからの小さなずれの効果がいろいろ現れてきて,重要なことがかえって隠される可能性が出てきます.念入りに準備して十分な工夫を凝らした実験でなければ,絶対零度での最低エネルギー状態について確かな知識を得るのはますます困難になり,付加的要因の影響に悩まされることになります.そんな困難に立ち向かうのも研究の醍醐味の1つですが,前提になる主要なポイントをまずはっきりさせておかなければ,よりどころがなくなってしまいます.もっと低温へ,というのは高温のようすがだいたいわかって,次に何を捜すべきか自覚している場合の話です.まあ,案ずるより産むが易しということもあって,捜し物が大物(新超伝導体とか)であれば,そんなことは見つけたあとでじっくり考えればよいし,実験進行中ならばできることは低温まで全部やっておくのが正しい態度ですが.

ここでいったことは高温展開という考え方ともマッチしています.高温展開を最初の1項でやめてしまえば,それはキュリー則を与えます.常磁性のスピンがあるというだけのことです.高温展開では,以下,あるスピンと隣のスピンの間にある関係,あるスピンが隣を介してもう1つ隣のスピンとの間にもつ関係,...,というように近似を上げていきます.近くの重要なものから順に計算に繰り入れて行くわけです.最終的にすべてを取り込んでしまえるかどうか,は難しいところです.高温展開は 1/T = 0 を原点とする展開ですが,そこから見れば絶対零度(T = 0)は無限の彼方にあります.しかし重要な部分が取り込んであれば,それを対応する実験結果と比較して,信頼できる結論を下すことはできます.
低温のエネルギー最低状態から出発して高温にアプローチするやり方がないわけではありません.少なくとも絶対零度で磁気秩序ができていることを仮定すれば,スピン波理論を使ってその状態から少しずつスピンの向きをねじった状態のエネルギーを求めることができ,その磁気秩序の安定性や物性量の低温部の温度変化が評価できます.また,現実の結晶構造から取り出した一部についてコンピュータシミュレーションする方法もあります.実験との比較では,極低温になると子細な要因でも実験結果には大きな影響を及ぼすことや,エネルギー最低状態がどんな状態かわかっていない場合にまったく予想外の結果になりうることなど,十分な注意が必要です.
またしても蘊蓄が長くなってしまいました.磁化率の測定結果からわかることをひとまずまとめておくと,
今回のデータをごらんになった人から,一次元や二次元のフラストレーションのないモデルに何らかの調整を加えればこのデータも説明可能ではないのか,という意味の質問を受けることがよくありました.たしかに単に丸いピークが示す形だけ見ると,よく知られた一・二次元のものとよく似ていて,それでどうにか説明がつきそうな気もします.しかし定量的に見れば,三角格子の挙動とそれらは大きく異なり,もはや質的に違うとさえいえます.
まず,単に形が似ているということを越えて,ある理論モデルが磁化率の実験結果を説明する資格があるかないかを簡単に判別する原理を紹介しておきます.磁性体の物性量の温度変化は,熱エネルギー kT とスピン間に働いている力のエネルギー J との比,
t = kT/J = T/ (J/k)
の関数として表されます.温度 T そのものではなく,それを J/k という尺度で測ります.これで個別の系がもつ J の値に左右されず,同じタイプの系の磁化率を1つの関数χ J/k = 1(t )
で表せます.(専門家はこういうのを J でスケールする--- J を単位として物事を測る---といいます.つまり J/k = 1 としたということ.)同じ構造の物質AとBがあって,BがAの2倍のJをもつなら,Aの磁化率がある温度で何か特徴(例えば極大や変曲点)を示すとき,Bはその2倍の温度で同じ特徴を示すということです. 一方,極限 T --> ∞(t --> 0)で磁化率χは必ずキュリーの法則χ(T ) = C/T
に従います.(これは十分高温ならどんな気体も理想気体の状態方程式に従うという話と同様のことで,つまりキュリーの法則は理想常磁性体の状態方程式です.)C はJ とも T とも無関係な,個々のスピンの性質だけで決まる定数です.(気体にも気体定数 R というのがあります.)t を変数としてキュリーの法則を書き直せば,(J/k )χ = C/ (kT/J) = C/t
となります.この式が,χJ/k=1(t )がt --> 0の極限で正しくキュリーの法則を与える形です.このことから,χJ = 1(t) = (J/k)χ
がわかります.念のため,ここで高温の極限をとっているのは(結晶構造はそのまま保ってスピンの熱運動だけ激しくするという)思考実験の話で,本当に1000度とかに試料を加熱すると,もちろん分解してめちゃくちゃになります.
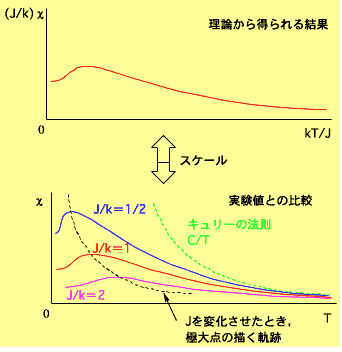
さて,χJ/k = 1( t )が t = X で値 Y をとるとします.スピン間に J が働く具体的な物質でこれがどう見えるかというと,温度 T = (J/k)t で磁化率がχ = Y/ (J/k ) になります.つまり,同じモデルで表される物質での J の値による違いは,( J/k = 1 の場合と比べると)温度が J/k 倍に,磁化率が k/J 倍になるとすれば得られます.例えば磁化率の最大値に目をつけると, J が2倍になれば,最大値χmaxは1/2倍,最大値をとる温度 Tmax は2倍になります.そこで,磁化率を温度に対してプロットしたグラフでは,最大値は一定の軌跡
χmaxTmax = 定数,
の上(少なくとも近く)を通るはずです.大きくはずれているようなら,その実験結果にそのモデルを適用するのは大きな間違いです.上記のことを知った上で今回の測定データと理論モデルを比較すれば,フラストレーションのないモデルはまるでダメだ,ということがわかるでしょう.前節で「この瞬間,筆者はフラストレーションの効果がデータに現れていることを確信しました.」と書いたのは,この判断に基づいてのことでした.データ取扱いの訓練が積んであれば,文字通り瞬間的にできる簡単な判断です.コンピュータにかけてみないと判断できないのは素人です.
こういう着眼法は教科書にはあまり書いていないことですが,磁性の研究で実験データを見るときには一番大切かつ有用なことです.しかも磁性に限らず物理全般に応用できる考え方です.磁性なら磁性について専門的になるということは,測定装置をもっているとか磁性体物質をいじっているとかいうことだけではなく,ここで述べた類のいくつかの着眼がすぐに迷わずできるようになるということだと思います.こんな簡単なこと(何しろ乗除算だけです)が理解できない自称専門家がいたりするのは,それこそ理解できない残念なことです.
では,フラストレーションの有無で,磁化率の挙動がなぜこんなに違うのでしょうか?フラストレーションがない反強磁性系は一般に次のような性質をもちます.1つのスピンが感じる相互作用は,その周りの隣接スピンの数を z とすると zJ で,スピン1/2のときなら T = zJ/4k 付近を境にして系の性質が変わります.たとえば三次元系では,この温度付近で相転移を起こし,隣接スピンが逆向きに整列した反強磁性状態になるので,高温からここまで増加してきた磁化率が突如減少に転じ,下向きに折れ曲がります.一次元(z = 2)や二次元(z = 4)では相転移は起きませんが,この温度以下で隣接スピンどうしが逆向きになる傾向(反強磁性相関)が顕著になるので,やはり磁化率は減少に転じます(折れ曲がりはない).極大値の出現はこのことを示しています.詳細は系の形や次元によって異なりますが,T = zJ/4k 付近に極大なり屈曲なりの特徴が現れることは共通しています.この温度以下で,スピンが感じる相互作用がそれを乱す熱エネルギーに打ち勝つのです.
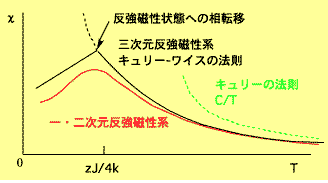
しかしフラストレーションが強く働いている三角格子( z = 6)の場合,T = zJ/4k 付近には特徴がなく,磁化率は低温に向かってそのまま増大していきます.その1/3以下の温度まで下がってから,ようやく極大を示して減少に転じます.これは大変もっともらしいことで,熱エネルギーだけでなくフラストレーションも反強磁性相関の発達をじゃましていることを表しています.もっとはっきりいうと,フラストレーションがあればあたかもその分だけ温度が高いように見える,ということです.
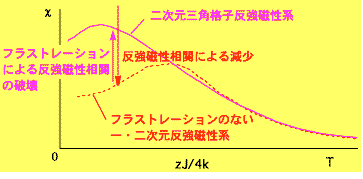
今回の実験で観測された最も重要なことはこれで,磁化率を押し下げる反強磁性相関がフラストレーションに妨げられたために,(相互作用の強さ J に比べて)ずっと低温まで磁化率が増大し続けるのが実際に見られた,というのが第一のポイントです.三角格子から大きくはずれていれば,フラストレーションのない一・二次元のモデルに近づくはずです.事実はいずれでもないから,今回測定した5種の [Pd(dmit)2] 塩は少なくとも三角格子に近いものといえます(そう考える以外説明のつかないデータを得た).これらの基底状態はどうなっているか,も重要な問題です(次に触れます)が,今それよりも重要なことは,これまで現実の物質では誰もはっきり認識したことがなかった現象=フラストレーションのせいで磁化率がかなり低温まで増加し続けたこと=をはじめて確認した,ということです.これによって,ある物質が三角格子としてのフラストレーションをもっているかどうかは,磁化率の温度変化を追跡すればわかる,という指針が実証・確立されたことになります.
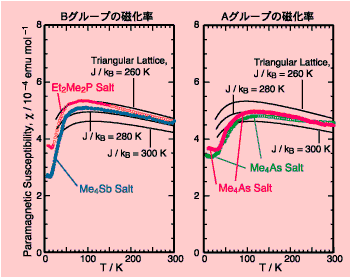
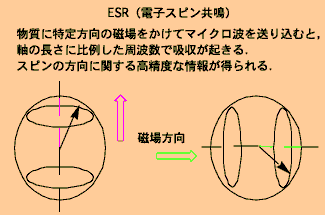
(CH3)2(C2H5)2Sb塩を除いて,磁化率の実験データには反強磁性状態への転移が現れています.実はここに反強磁性転移があるということは,ESR(電子スピン共鳴)という実験によって以前から明らかにされていました.それを再確認したにすぎない,といえばそうなのですが,
まず転移が起きるための基本条件を1つ挙げておきます.それはマーミン-ワグナー(Mermin-Wagner)の定理というもので,「連続対称性をもつスピンの一次元・二次元の系は有限温度では長距離秩序をもたない」との内容です.
ちょっと解説しておきましょう.連続対称性とはスピンの状態(↑とか↓とか)を指定する軸の方向を連続的に変化させることが可能ということです.ふつうの有機分子上のスピンはハイゼンベルク型で,これは連続対称性をもっています.世の中には変わったスピンもあって,分子や結晶に対して特定方向の軸に沿った成分しかもたないイジングスピン(スピンがz成分だけもつ)というのもあります.イジングスピンの系の磁化率を測ると,z方向に磁場をかけたときだけ磁化率が大きく,ほかの方向では磁化率がほとんどゼロになります.こういうのを磁気異方性と呼びます.実はイジングスピンが現れるのは,電子の軌道角運動量(原子の周りの公転運動)の特定成分が本来のスピン(電子の自転)と混じってしまった結果です.多くの有機分子では軌道角運動量は消滅していますので,イジングスピンのようなものは考える必要はあまりなく,本来の電子スピンを表すハイゼンベルクスピン(スピン状態を指定する軸はどっち向きでもよい=スピンはxyz3成分のベクトル)で考えて問題ありません.[Pd(dmit)2]塩の場合も,ハイゼンベルクスピンと考えて問題ないことは,ESR実験から求められるg因子が磁場方向を変えてもあまり変わらないことからわかっています.しかし,ごくわずかなハイゼンベルクスピンからのずれというものは,どんな物質であれ常に存在し,極低温で問題になる可能性はあります.
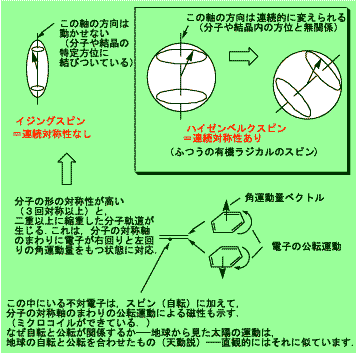
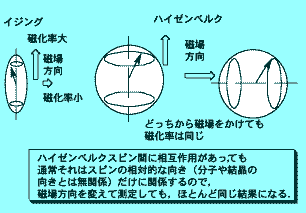
次に,有限温度とは絶対零度以外という意味です.長距離秩序とは,スピンの向きの相関(例えば↑の隣は↓,そのまた隣は↑...という相互関係)が試料の端から端まで減衰しないで続いているということで,ふつうに秩序といえばこれのことです.整列といってもよいでしょう.エントロピーはほとんどゼロになります.これに対して短距離秩序とは,↑の隣は1/2より大きな確率で↓となり,もし↓だとするとそのまた隣は1/2より大きな確率で↑...というように,秩序(この場合は反強磁性相関)が未完成で発達中の状態であり,すぐ隣どうしの関係についてはまあまあはっきりしたことがいえますが,遠くの関係についてはたしかなことはいえず,まだいろいろな可能性が許されていてその間を刻々と変化しているわけですから,エントロピーはゼロまでは減少しません.スピンのかわりに分子の位置を考えてみれば,これは結晶固体と液体の違いのようなものです.液体の短距離秩序とは,接している分子の数や分子間距離で,ほぼ一定ですが揺らいでいます.長距離秩序のできている系の一部に弱い外力(熱・磁場など)を加えると秩序は乱されますが,外力を除いてやれば元の状態に回復します.短距離秩序の場合はそうはいきません.固体を変形させても弾性限界内なら元に戻りますが,液体には変形からの回復力はありません.長距離秩序ができるときには相転移が起きて元の状態と明確な境界(転移点)で隔てられますが,短距離秩序は連続的に発達するだけで相転移は起こしません.物質の温度を下げていくとまず短距離秩序が発達して,さらに低温で可能ならば長距離秩序を起こします.マーミン-ワグナーの定理の主張は,一次元や二次元では,長距離秩序の回復力が弱すぎて,わずかでも熱エネルギーが加わると壊れてしまう,ということです.

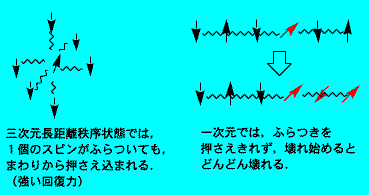
マーミン-ワグナーの定理によれば,フラストレーションがあろうがなかろうが,二次元ハイゼンベルク系では反強磁性転移は絶対零度まで現れないはずです.しかし(CH3)2(C2H5)2Sb塩以外では反強磁性転移が現れています.なぜでしょうか?現実の[Pd(dmit)2]塩の結晶は,もちろん純粋な二次元ではなく,層が積み重なった三次元系です.層内のスピン間に働く力が層間で働く力に比べて圧倒的に強いので,二次元としてモデル化したわけです.このように非常に二次元に近いものでも,ずっと低温にすると層間相互作用が熱エネルギーに打ち勝って物性量に影響してきます.ある程度の温度以下では二次元ではなく三次元の系としてふるまいます.
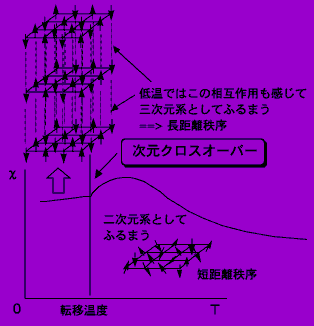
このような現象を次元クロスオーバーと呼び,一次元や二次元に近い系でよく見られます. [Pd(dmit)2] 塩の磁化率は,ずっと高温から層内の相互作用に支配されていますが,層間相互作用の影響は磁化率のピークよりも低温側でようやく現れてきていると考えられます.このような物質の例は,層状の正方格子構造をもつ銅(II)化合物などでたくさん知られていて,二次元正方格子モデルに従って磁化率ピークを示し,そのずっと低温側で反強磁性転移を示します.このような物質の小さな結晶を多数集めて磁化率を測定すると(磁化率の方向による平均の測定),転移温度以下でほぼ一定の磁化率がしばしば見られます.これはハイゼンベルクスピンの層状化合物に共通した性質と考えられ,教科書的な平均場理論による予想=絶対零度で転移点での磁化率の2/3の値をとるように直線的に減少=とは異なります.[Pd(dmit)2] 塩の磁化率もそうなっています.
層間の相互作用が反強磁性秩序にとって必須であることは前提です.しかし [Pd(dmit)2] 塩の結晶構造を調べても,層間の相互作用はごく小さく,系統的な差異ははっきりしません.ほかに転移温度に影響を与える要因はないでしょうか?フラストレーションの強弱がそれであろうと考えています.層間の相互作用が働いたとして,実際にある温度で反強磁性秩序を起こすためには,その秩序状態で十分なエネルギーの利得(その温度で秩序化しないで得られるエントロピーによる得 TS を上回るだけの)が必要です.フラストレーションがあると,スピンは妥協を強いられて,仮に秩序化しても十分なエネルギーの利得が得られません.秩序化によるエネルギー利得は,フラストレーションのある三角格子からはずれてフラストレーションなしの正方格子に向かうと増加し,それだけ秩序状態が安定になっているはずです.そうすると秩序化する温度も上がるであろうと考えられます.実験で見られた転移温度は,結晶構造などから三角格子からずれていると推定されているものほど高くなっています.
このことについて数字の上できちんとした結論を下すには,三角格子からのずれとともに層間の相互作用も含めて,他の実験結果とも比較しながら,磁化率の温度依存性をさらに詳しく解析する必要があります.
[Pd(dmit)2] 塩では,フラストレーションが強い(正三角格子に近い)と推定されるものほど,圧力をかけたときにモット絶縁体状態が壊れて金属伝導が生じやすい,という傾向が見られます.いままでの有機導体では,金属になるかモット絶縁体になるかという問題は,電子が自由に分子間を動き回れる度合い(バンド幅=共鳴の強さ)とその運動を妨げる分子内の電子2個の反発力との競合で,とらえられてきました.しかしどうやら [Pd(dmit)2] 塩ではそれだけでは片づかないようなのです.というのは,結晶構造から判断すると金属になりにくいものの方が逆にバンド幅が大きい傾向があるからです.
モット絶縁体の温度を下げていくと,最終的には反強磁性秩序が形成されて,エネルギーが最低になります.前節で触れたように,フラストレーションがあると,その際にあまりエネルギーが下がらないはずです.これはモット絶縁体状態が相対的に不安定になっていることを意味します.そこでもし,バンド幅(金属伝導状態における共鳴エネルギーの利得)が少しばかり増えたりして金属伝導に有利な方向に動けば,フラストレーションのないものよりも容易に金属状態に変わると考えられます.一連の [Pd(dmit)2] 塩に見られる傾向はこのようなシナリオを示唆しているように見えます.
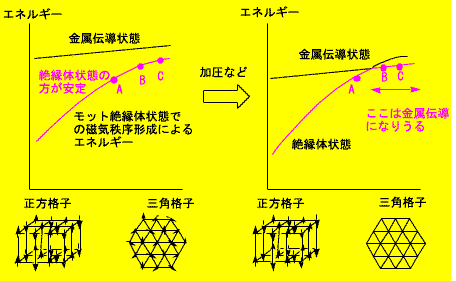
これが本当なら,モット絶縁体になるか金属になるかという重要な問題を解く鍵として,バンド幅と電子間反発に加えて,もし存在すればフラストレーションの度合いも考えるに値する要因だということになります.フラストレーションの度合いは,分子の配列パターンによって敏感に変化するので,物性と物質構造の多様性のかかわりを活かしていく上ではとても魅力的な話です.本当にこんなことが起きているのかどうか,それを確かめるには,圧力をかけた状態で [Pd(dmit)2] 塩の構造・電気伝導・磁性を総合的に詳しく調べる必要があるのは当然です.
最後に,電子物性の温度変化の一般論から,フラストレーションの果たす役割を少し考えてみます.どんな物質でも,温度を下げていくと,エントロピーの低い状態に向かっていきます.金属の伝導電子の場合は,フェルミ統計の効果で,エントロピーは温度に比例して順調にゼロに向かいます.そんなふうにすんなり行けば何も起きないのですが,強相関電子系で電子が動けなくなっていてスピンが回転するだけの場合,もしスピン間に働く力が非常に弱ければ,低温になってもエントロピーがなかなか下がりません.スピンは,秩序をつくってエントロピーを下げようとうずうずしているのですが,ちょっとした熱エネルギーでもそれが壊されてしまう,という状況です.ようやくスピン間の力が熱エネルギーに勝てるようになると,一気にエントロピーを放出し,物性量は激しく変化します.そのときが来るまで,スピンの方では(エネルギーは当然上げないで)何とかエントロピーを下げる方法はないかと,うずうずしながら,ときには物理学者の考えの及びにくいようなやり方も探っています.
量子力学の効果を使う,というのもその1つです.スピンが独立にふるまっているからエントロピーが大きいわけで,もしスピンが結合電子のように2個ずつでペアを組んで1つの状態をつくってしまえば,途端にエントロピーはゼロになります.中にはとても変な結合をつくる状態があります.動かない電子と伝導電子が両方あるような物質では,動かない電子のスピンがほかの伝導電子を1個引き寄せて結合してしまったりもします(これを近藤効果と呼びます).超伝導もその類で,温度に比例するエントロピー減少でもまだ飽き足らない電子は,結合距離不定のペアを組んで,ペアの重心運動に対応する位相を揃える,という変なやり方で,強引にエントロピーを下げてしまいます.
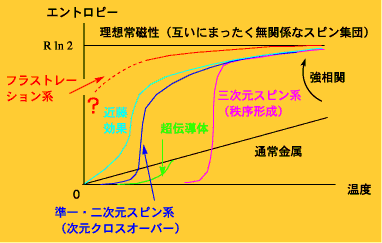
こういう奇妙な,つまり面白い現象が起きるには,電子のエントロピーが順調に下がっていくような場合よりも,電子が無理にエントロピーを貯め込んだまま低温にもって行かれた状態に追い込まれていることが必要です.追い込まれた電子は,何か奇妙な手を使って脱出を試みる,それを見てやろう,というわけです.電子系が強相関になっていて自由にエントロピーを下げられない,というのも重要な条件になります.この場合は,スピン間に働く力を利用して反強磁性秩序をつくってエントロピーを下げようとするのがふつうです.(正方格子の磁化率が,反強磁性相関の効果を示して低温で減少していくのもそのためですが,純二次元系では短距離秩序が発達するだけで,絶対零度になるまでエントロピーはゼロになりません.)しかしフラストレーションが効いているとどうでしょうか?スピン間に強い力が働いていても,それがお互いに妨害しあっているので,反強磁性相関はなかなか発達せず,かなり低温になってもエントロピーはあまり減少しません.無理にエントロピーを下げようとするとエネルギーの方が上がってしまうという状況です.電子は文字通りフラストレーションを抱えているわけで,何か抜け道を探っているはずです.無理矢理に反強磁性秩序を形成して我慢する.あるいはいっそのこと動き出して伝導電子になってしまえば,スピンのフラストレーションは消えてしまいます.それが1つの可能性かもしれません.するとその先には何があるのか....
実をいうと我々は,エントロピー効果が絶縁体状態から金属伝導状態への引き金の役割を果たしている実例を,分子性伝導体の中にすでに1つ知っています.それは DCNQI というアクセプターと銅の化合物の,(DCNQI)2Cu という物質です.ある条件で,この物質は温度を下げると金属状態から絶縁化し,もっと低温でまた金属状態に復帰するという奇妙な振る舞いを見せます.金属状態ではDCNQI上の電子も銅イオンの電子も混じり合って伝導電子になっていますが,絶縁体状態ではDCNQI上の電子は結合対をつくってしまい,銅イオンに不対電子が取り残されて常磁性になっています.(銅の部分は強相関でモット絶縁体=常磁性になっていると見てよい).東邦大学の梶田教授・西尾教授らによる高感度比熱測定 (Y. Nishio et al.: J. Phys. Soc. Jpn. 69 (2000) 1414.) により,絶縁体状態と金属状態とのエントロピー差が求められ,金属状態のエントロピーは絶縁体状態に比べて温度にほぼ比例して減少していくことが示されました.(そのうち半分程度が金属伝導電子の寄与で,残りは分子の振動が絶縁体と金属状態でわずかに異なっている分です.)これは,適当な条件の下で,高温と低温の両側で金属状態の自由エネルギーが絶縁体状態のものより小さくなることを意味し,観測された奇妙な振る舞いを説明します.常磁性絶縁体ではエントロピーが下げられず,低温でエントロピーが低くなる金属状態の方が選ばれたのです.(これと似たもの---というより歴史的には先輩---には,液体ヘリウム3というものがあり,極低温では量子効果で液体の方が固体よりエントロピーが低くなるので,いったん凝固したものがさらに低温で再び融解します.)実際,絶縁体状態のままでも反強磁性秩序が生じてエントロピーを下げられる条件にすると,低温で金属状態は現れません.(DCNQI)2Cuでは,高エントロピーのまま低温に追い込まれた電子系が,反強磁性秩序をつくるか金属伝導に戻るかの択一を迫られているところを明確に観測できました.なお,筆者は(DCNQI)2Cuの磁性の研究で8年前に,の3つの発見をしましたが,(2)と(3)のメカニズムに対しては今に至るまで満足な説明がありません.(3)など,強相関の伝導電子系の性質が最も顕著に現れている実例なので,意欲的な研究者の取り組みを期待しています.
- (1) 金属-絶縁体転移に伴う磁化率のスイッチ的変化 (M. Tamura et al.: J. Phys. Soc. Jpn. 63 (1994) 429.),
- (2) 反強磁性秩序状態に伴う弱い強磁性 (M. Tamura et al.: J. Phys. Soc. Jpn. 62 (1993) 1470; 63 (1994) 425.),
- (3) 一部の化合物の金属状態に現れる磁化率の強い温度変化 (M. Tamura et al.: Solid State Commun. 93 (1995) 585; Mol. Cryst. Liq. Cryst. 285 (1996) 151-156.),
電子系を追い込んで何か奇妙な振る舞いをさせる状況としてフラストレーションを見るのは,大変興味深いことです.そのためにはフラストレーションが実際に働いているのを確かめるのが先決です.今回の研究の意義は,[Pd(dmit)2] 塩という物質でそれを確かめた,ということです.