私たちのグループは、計算機や数理的手法を用いて、生命現象に取り組んでいます。特に多量の情報を統合して高次生命現象を理解する場合や、時空間中にパターンが展開する形態形成現象を理解するうえで、数理的手法は有効だと考えています。
現在の研究内容
神経細胞樹状突起パターン
ある種の神経細胞は、樹状突起を曲面上で、むら無く一様に分布させることから、space filling typeと呼ばれる。この樹状突起は、一様分布の生成に加えて、空間分割、突起の再生など、様々な空間秩序を生成できる。我々は、神経細胞の空間秩序の原理を、理解する数理モデルを構築し、解析した。2次元平面を細胞内と細胞外の二つの領域に分け、細胞領域が拡散性の因子の制御を受けて成長すると仮定する。樹状突起の成長を促進する活性化因子と、成長を抑制し、突起間相互作用に関わる抑制因子を考慮し、反応拡散方程式の拡張モデルを構築した。解析により、樹状突起がもつ空間制御、一様分布、空間分割、再生が、同一の仕組みによって理解できることを示した。また、樹状突起の外形と細胞内の活性化因子の分布との間に強い相関が有ることも分かり、活性化因子が連続的に分布するときには外形はスムースになり、不連続に分布するときには外形は乱れることを示した。この相関は実際の神経細胞でも存在する可能性がある。本研究は、京都大学の上村匡教授、杉村薫研究員と、理論生物学研究部門との共同研究である (Sugimura K., Shimono K., Uemura T. and Mochizuki A (2007) Self-organizing mechanism for development of space-filling neuronal dendrites. PLoS Comput Biol. 3(11), 2143-2154.)。
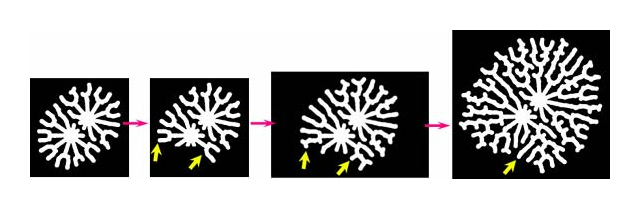
図1. 樹状突起パターンの例
現実の樹状突起で見られるような空間秩序を、数理モデルは再現する。この図では二つの細胞が、それぞれの周囲に樹状突起を一様に展開する一方で、互いに接触を避けあうことにより、空間分割を示している。また突起の一部を削除することにより、突起の再生と一様分布の再構築も起こる。
