私たちのグループは、計算機や数理的手法を用いて、生命現象に取り組んでいます。特に多量の情報を統合して高次生命現象を理解する場合や、時空間中にパターンが展開する形態形成現象を理解するうえで、数理的手法は有効だと考えています。
過去の研究内容
線虫の温度走性
多くの生物は環境温度に対する適応戦略を持ちますが、線虫も例外ではありません。線虫は生育温度を記憶しており、餌条件に応じて好みの温度帯が変化します。温度走性とは適温に向かって移動する性質を指しますが、我々の研究はその温度走性を対象としたものです。
線虫を集団で観察すると生育温度に向かう行動が観察できることが知られていましたが、ここ数年で一見矛盾するような異なる観察結果が報告され、議論となりました。我々は実験観察から得られた運動や神経活動についてのデータを総合し、さらに未知の部分については仮説をおくことで温度走性行動に対する統合的な数理モデルを構築しました。 数理モデルを解析したところ、
- 矛盾するように見える観察結果には実は矛盾がない
- 実験条件によっては、異なる観察結果が得られる
といった結論と予測を得ました(Nakazato K. and Mochizuki A. (2009) Steepness of thermal gradient is essential to obtain a unified view of thermotaxis in C. elegans, J. theor. Biol. 260, 56-65.)。なお、この結果は実験との整合性を確認済みです。
このような一見矛盾した観察結果は、線虫の動きのランダム性に由来しています。ランダム性のある現象は適切な条件設定の下で多くのサンプル集団を 用意して初めて正確な特徴を掴むことができますが、線虫の温度走性は単純ではなく、条件ごとに異なる側面を示すのです。
現在、画像解析技術などを使って大量の線虫集団の動きを捉える方法を開発しており、線虫の行動の詳細に踏み込んだ解析を行っています。

図1.
観察データの総合により構築した数理モデルと温度ダイヤグラム。線虫の運動は温度領域ごとに異なるが、原則としてランダムウォークで記述可能であると考えられてきた。線虫の移動はランダム性からのずれ(バイアス)による。バイアスの程度は温度の関数として表わされる。
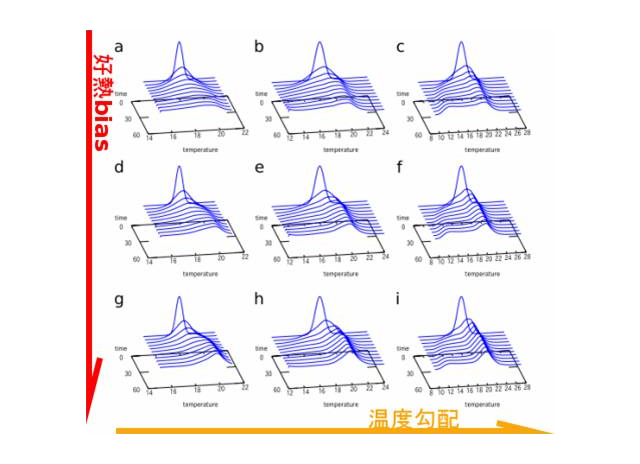
図2.
線虫集団分布の移動の推移。左手から右手に向かって温度軸。奥から手前に向かって時間軸。線虫の移動傾向は温度勾配方向のバイアスと温度勾配率の両方に依存する。好熱方向への移動は温度勾配率が十分に緩やかな場合に観察可能である。
