私たちのグループは、計算機や数理的手法を用いて、生命現象に取り組んでいます。特に多量の情報を統合して高次生命現象を理解する場合や、時空間中にパターンが展開する形態形成現象を理解するうえで、数理的手法は有効だと考えています。
過去の研究内容
魚類網膜の錐体細胞モザイク
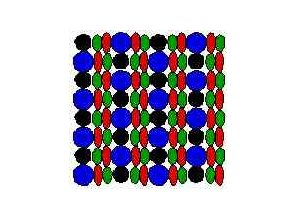
魚類の網膜で、異なる周波数の光に対応する錐体細胞がモザイク状にきれいなパターンを形成している。各種の錐体は2次元平面上で周期的に現れる。このパターン形成のメカニズムは明らかでないが、未分化な(周波数特異的opsinを発現していない)細胞がランダムに分布している初期状態から、モザイクパターンが作られている。Zebrafishのモザイクに注目し、異なる仮定に基づく2つの数理モデルを作った。
未分化であるが規則的な細胞分布が実現した後に錐体の種類の分化の運命が決まるモデルと、あらかじめ分化した細胞が細胞再配列によりパターンを作るとするモデル(Cell Sortingモデル)を解析した。 どちらも最近接相互作用(たとえば細胞間接着力)が働くとする。例えば細胞選別モデルでは、細胞間接着の合計の大きさを増加させる方向に、より細胞移動が起こりやすいとした。
それぞれについてモザイクができる条件が得られた。ダブルコーン(赤錐体と緑錐体とが繋がった構造)を考慮すると現実のZebrafishとおなじパターンが得られる。上図はCell Sortingモデルによるもの。
