研究紹介

変分モンテカルロ法を用いた強相関電子系の研究

変分モンテカルロ（VMC）法は、電子相関のある系の基底状態の性質を調べることが強力な計算手法となっています。この手法では、基底状態をある適切な試行関数として仮定します。試行関数の物理量は、モンテカルロシミュレーションを行う事で、統計誤差の範囲内で厳密に求める事ができます。負符号問題が起こらないので、フラストレーションのある系、多軌道系など、非常に幅広い研究分野に応用する事ができる事が、この手法の魅力となっています。

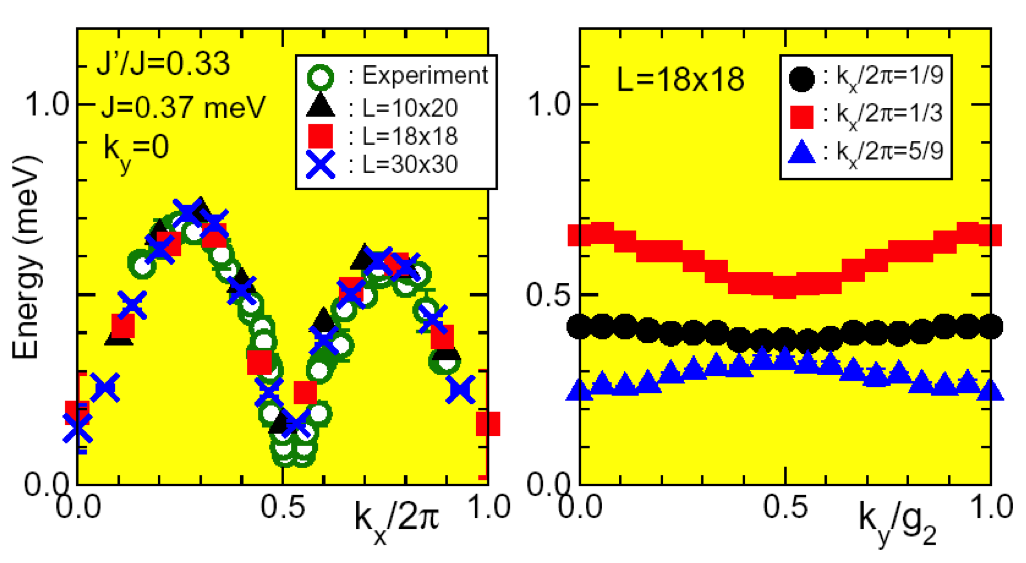
図：VMCを用いて計算された、異方的三角格子スピン1/2ハイゼンベルグ模型の低エネルギー励起スペクトル。

イリジウム酸化物の理論的研究

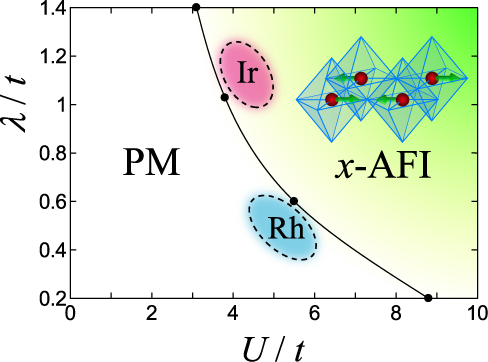Sr₂IrO₄ は、5d-電子系特有の大きなスピン軌道相互作用によって誘起された新奇モット絶縁体と考えられています。この、スピン軌道相互作用誘起モット絶縁体の発現機構を明らかにする為に、我々はスピン軌道相互作用を含む３軌道ハバード模型を調べました。我々は、変分モンテカルロ法を用いて、基底状態の相図(右図)を調べ、クーロン斥力（\(U\)）とスピン軌道相互作用（\(\lambda\)）が協力的に働き、金属-モット絶縁体転移を導く事を明らかにしました。軌道とスピン両方からなる全磁気モーメントは、２次元平面上で汎強磁性的に秩序化しています。我々の結果は、4d電子系の\(U\)が大きく\(\lambda\)が小さい物質 Sr₂RhO₄ の金属的振る舞いもよく記述できています。

図：スピン軌道相互作用を含む有効３軌道ハバード模型の基底状態相図。常磁性金属からスピン軌道誘起モット絶縁体 (x-AFI) への転移が\(U\text{-}\lambda\) 平面上で示されている。

光格子中の冷却気体

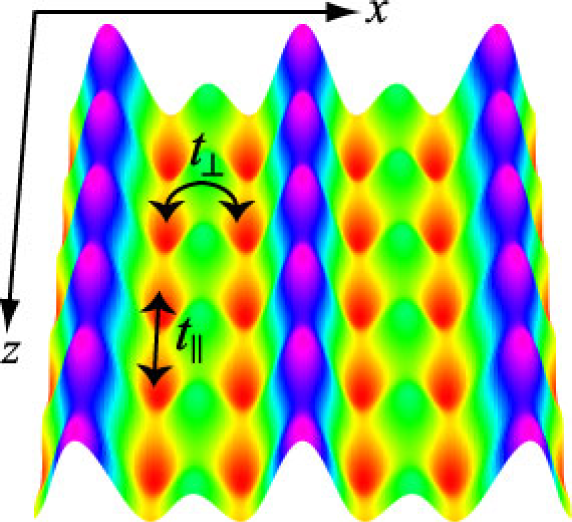光格子はレーザー光の定在波で作られ、原子に対してcosine型の周期ポテンシャルとして作用します。この光格子中に閉じ込められた原子気体系は、固体中の電子系や液体ヘリウム系などの凝縮系と多くの点で類似していて、この系の物性を詳細に理解することが凝縮系の物理の深い理解につながります。さらに、光格子系では格子の深さと構造、原子のスピン自由度、原子間相互作用の強さを幅広く精密に制御することができるので、従来の凝縮系では到達できなかった極限的な領域まで達することができ、そこで新奇な量子相、量子相転移、トランスポート、非平衡ダイナミクスが実験・理論の両面から研究できます。我々は、時間依存密度行列繰り込み群法、変分モンテカルロ法、朝永-ラッティンジャー流体理論などの量子多体理論を用いて光格子系を研究しています。特に、強相関領域における超流動体の物性とダイポーラー気体（強い双極子モーメントをもつ粒子からなる気体）超流動固体相に関して詳細に調べています。

図：２重井戸光格子によって作られた２本鎖梯子格子構造。

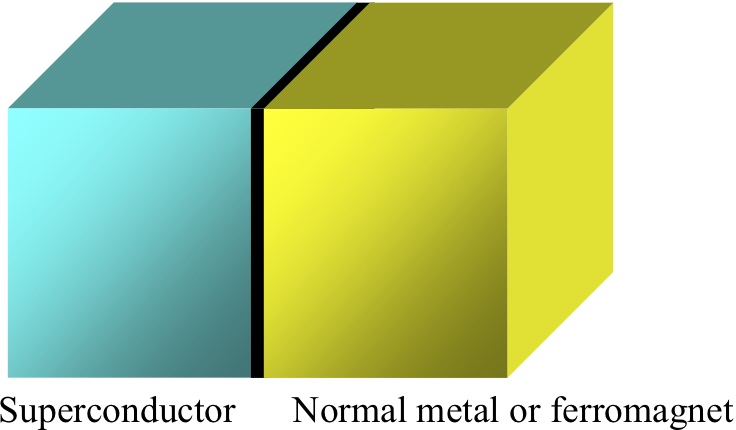
超伝導体を含むナノ複合構造におけるスピン依存伝導現象の理論的研究

左図:超伝導/常伝導(強磁性)接合の概念図。

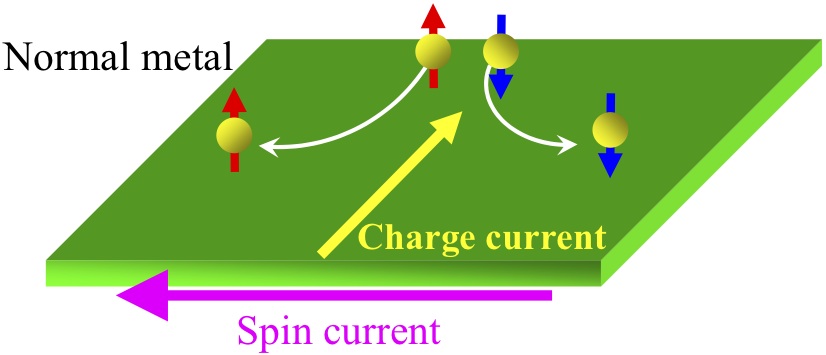
右図:スピンホール効果の概念図.　物質中のスピン軌道相互作用によって電流がスピン流またはその逆過程が生じる。

我々は、超伝導体と常伝導体または強磁性体から構成されるナノ複合構造(左図)において出現する、スピン依存伝導現象を理論的に研究しています。特に、スピンホール効果(右図)やスピン蓄積に関する研究を中心に行っています。更に、ナノ複合構造において出現する物理現象を用いた新しいナノデバイスの提案も行っています。計算手法は、非平衡Green関数法および準古典Green関数法などです。

金属接合における熱電能の第一原理計算

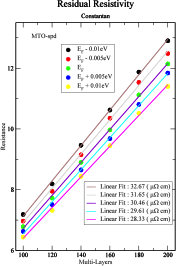金属接合におけるペルティエ効果の定量的解析のために、我々は、タイトバインディングマフィンティン軌道を基底に使った密度汎関数理論の枠組みをもとにした第一原理計算によって、バルクと接触界面に対する熱電パラメータを定量的に見積もりました。量子輸送係数の計算には Landauer-Büttiker 形式が用い、量子散乱のエネルギー依存性には、有名なモット則によって決定しました。バルクCuNi(コンスタンタン)合金の電気抵抗は、厚みの関数とした全抵抗の傾きから与えられ、その値はフェルミ準位で 30.46 µΩcm 程度になりました(右図)。このとき、室温 (T) での熱電能 (=–S/T) は 171.75 nV/K²程度となりました。 CuNi/Au 接合の場合、見積もられた接触界面での熱電能は100 nV/K²程度となり、これはバルクの値と比べて著しく大きい事がわかりました。それゆえ、我々は、金属接合における接触界面の熱伝導への寄与は、従来考えられてきたものよりもっと重要で、より定量的な理論計算と実験結果の比較を検討する必要があると考えています。

図：フェルミエネルギー付近の異なるエネルギー準位に対する厚みの関数としてCuNiの抵抗値。

遷移金属タンパク質とハルデン-アンダーソン不純物模型

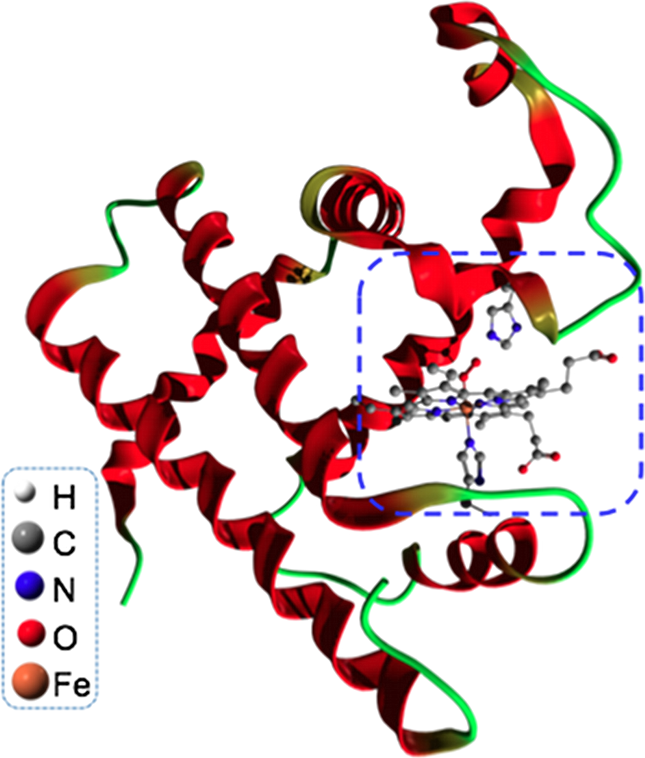ヘム金属タンパク質は呼吸やエネルギー生産などの生体内作用で中心的役割を担う、重要なタンパク質です。例えば、ミオグロビン、ヘモグロビン、シトクローム、P450などがあります。このようなタンパク質の生物的活性は、主に、プロフィリンの活性中心に位置する遷移金属のスピン状態と局所的電荷によって決定されています。しかしながら、もっとも一般的な（例えば、密度汎関数法などの）第一原理計算手法は、多くのポルフィリンの基底状態に対して、誤ったスピン状態を予測してしまう事がよく知られています。なぜなら、これらの手法は遷移金属の電子相関を適切に記述できないためです。そこで、我々の計画では、第一原理密度汎関数法と量子多体模型計算手法を組み合わせることで、この問題に挑戦しています。まず、単純化されたミオグロビン模型（より複雑な活性サイトをポルフィリンに、近接ヒスチジンをイミダゾールに置き換えたもの）の第一原理的基底状態を、密度汎関数法の範囲内で得る為に、Gaussian 03 を使います。このミオグロビン模型に対する生物学的関連性の深い分子（例えば、O₂やCO）のボンディング効果を調べます。これらの分子が作る”バンド“を用いて、我々は周りを分子に囲まれた中心にある遷移金属のためのハルデン-アンダーソン不純物模型を構築します。ポルフィリンリングにおける多体効果を精密に考慮するため、量子モンテカルロ法や密度行列繰り込み群法などのような量子多体計算手法を用いて、我々はこの５軌道ハルデン-アンダーソン不純物模型を解きます。

図：筋組織呼吸作用などに関連するミオグロビン、プロテインの構造。活性サイト（青い点線内）は球と棒で表されている。

自己エネルギー汎関数法に基づく変分クラスター近似法とその応用

自己エネルギー汎関数法に基づく変分クラスター近似(VCA)法は、短距離の静的・動的相関の効果を厳密に取りいれた自己エネルギーを用いる手法であり、平均場を超える多体問題の計算手法として、近年注目を集めています。手法の応用範囲は広く、高温超伝導体や有機導体など、多様な相が競合している系を調べるのに適しています。この手法を用いて、我々は、強相関電子系における新奇量子状態を求めて、3d 遷移金属（銅酸化物、鉄系超伝導体）、5d 遷移金属（Sr₂IrO₄、右図）、グラフェンなどの強相関電子系の基底状態や低エネルギー励起の性質を調べています。

図: VCAで計算したSr₂IrO₄の一粒子励起スペクトル。

アンチペロブスカイト構造をもつ新しいタイプの３次元トポロジカル絶縁体

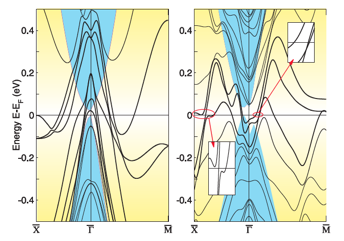これまでに実験的、理論的に発見されて認知されているすべてのトポロジカル絶縁体は、二つのタイプの結晶構造をもつグループに関連したもののみです。一つは、立方晶系の非中心対称なzinc-blend HgTeタイプ、もう一つは、六方晶系の中心対称なBi₂Se₃タイプです。本研究では、アンチペロブスカイト構造をもつ新しいタイプのトポロジカル絶縁体を提案しています。第一原理計算を通して、適切な１軸 strain の下で、立方晶系の３原子からなる中心対称なアンチペロブスカイト化合物 (M₃N)Bi（M=Ca, Sr, Ba）は３次元トポロジカル絶縁体となる証拠を示しました。我々は同じアンチペロブスカイト構造を持つその他の関連する物質も、どうように３次元トポロジカル絶縁体の候補となりうる事を議論しました。この提案された新しいタイプの物質は、化学的に不活性で、格子構造は重要な半導体をよくマッチするため、電気的デバイスを容易に構築するための豊かなプラットフォームを提供できます。

図: スピン軌道相互作用のある(Ca₃N)Biの(001)境界の電子バンド構造。左図は引っ張る力をかけない場合。右図はc軸方向を保ったままab平面を７％引き伸ばす力を加えた場合。

GPUにおけるカーネル多項式法の開発

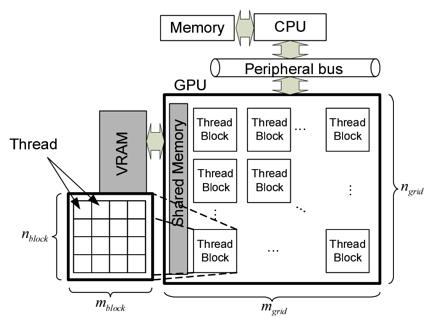カーネル多項式法（KPM）は、巨大なハミルトニアン行列の固有値を求めるための効率的な数値的手法です。チェビシェフ多項式と適切なカーネル関数を適用する事で、１粒子や２粒子の動的相関関数が制御可能な精度で効率的に求める事ができます。KPMの性能に関して、計算速度を向上させるためのGraphics Processing Units (GPU) やスーパーコンピュータを用いた大規模並列化は、より大きな系を扱う為に重要となってきます。我々の数値実験では、GPU上でのKPMの実効性能は、CPUを用いたものと比べて10倍以上よくなりました。この研究では、科学のグランドチャレンジ解決を手助けするためのGPUやCPUクラスター環境で応用できる、使いやすいライブラリーの構築を目指しています。

図: CUDAの実行モデル