We are studying many biological phenomena using theoretical methods, including mathematical and computational analyses. Theoretical methods are useful to decipher large amount of information, and to give an integrative understanding for the complex biological systems.
Present Works
Structure and dynamics of regulatory networks
Thanks to the progress of modern biology, we have many examples of large networks which describe regulations between a large number of species of molecules, such as genes, proteins or ions. It is widely believed that the dynamics of molecular activities based on such regulatory networks are the origin of biological functions. It is strongly expected to determine dynamics of biological systems from such static information of regulatory networks. However, we have to notice that the information on the regulatory network alone is not sufficient to determine the resulting dynamics. The regulatory edges only provide information on dependencies between activities of bio-molecules in the system. They lack essential quantitative details like the regulatory functions, parameter values of reaction rates, and initial states. "In silico" numerical simulations therefore rely on many unverified assumptions as to the regulatory functions and their dozens or hundreds of unknown parameters.
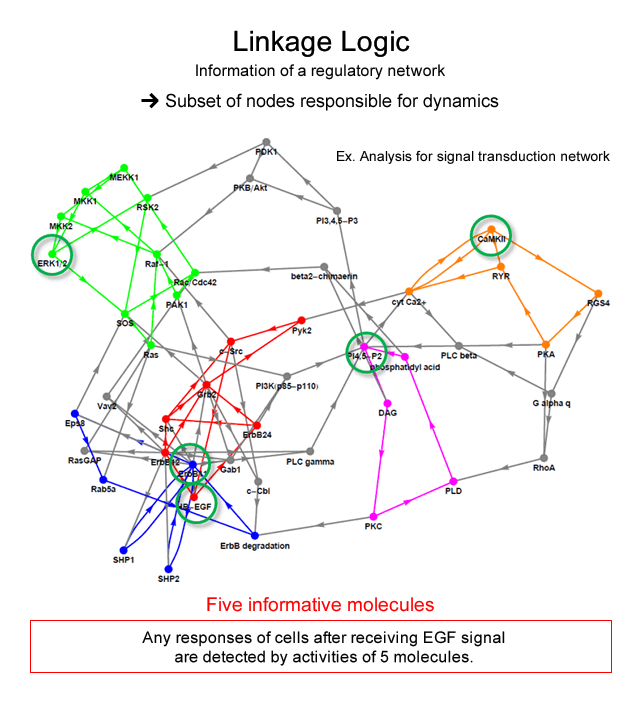
We solved this problem by changing our way of thinking: we may solve a mathematical problem "how much dynamical properties of a system can be determined from information of dependence between variables". Starting from this idea, we have developed a new theory to provide an important aspect of dynamics from information of regulatory linkages alone. The theory ensures that: i) any long-term dynamical behavior of the whole system can be identified faithfully by the measurement of only a subset of variables in the system, and that ii) the subset is determined from the regulatory linkage alone as a "feedback vertex set" (FVS) of the network graph. We also showed that controlling the dynamics of the FVS is sufficient to switch the dynamics of the whole system from one attractor to others, distinct from the original.
For example, the signal transduction network is known as a system for the determination of the macroscopic behavior of mammalian cells after receiving the signal molecule stimulus from outside. By the analysis of our theory, dynamical attractors possibly generated by a signal transduction network with 113 molecules can be identified by measurement of the activity of only 5 molecules, if the information on the network structure is correct. It implies that we will detect all of cell responses after receiving signal by measuring dynamics of 5 molecules.
We are now going to the next stage to progress our theory. We collaborated with some groups of experimental biology to verify our theory by qualitative measurements, and to analyze and understand dynamics of biological systems.