Cyanobacteria are the simplest organisms exhibiting circadian rhythms. In the bacterium, clock genes kaiA, kaiB and kaiC have been characterized as the indispensable clock regulators. KaiC plays a central role and exhibits rhythms in transcription, translation and phosphorylation status under continuous illumination conditions. The other clock proteins KaiA and KaiB modulate KaiC autophosphorylation: KaiA enhances autophosphorylation of KaiC, and KaiB inhibits this action of KaiA. It was recently revealed that periodic oscillation of the phosphorylation level of KaiC persists even under continuous dark conditions, where transcription and translation have almost ceased. The KaiC phosphorylation cycle was reconstituted even in vitro, thus confirming that the interaction between Kai proteins generates the cycle, although the specific mechanism that drives the clock remains unclear.

Using mathematical models, we investigated the mechanism for the transcription-less KaiC phosphorylation cycle.  We developed a simple model based on the possible KaiC behavior, which was suggested by previous experimental studies. In the model the KaiC-KaiA complex formation followed by a decrease in free KaiA molecules may attenuate the KaiC phosphorylation rate, and it acts as negative feedback in the system. However, our mathematical analysis proved that simple dynamics based on the experimentally suggested model converge to a stable equilibrium.

We then developed the generalized formulae of models and determined the necessary condition to destabilize the equilibrium of the system. Linear stability analysis revealed that destabilization can occur when there is sufficient distance of feedback between the recipient reaction and the effector.

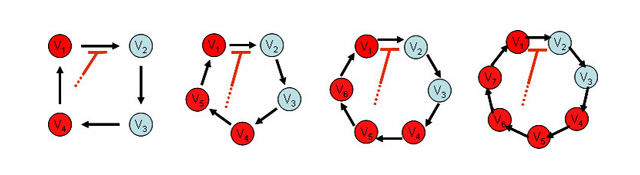
Figure 1.

Schematic representation of closed circuit model and the condition for the possible oscillation by inhibition of the transition from state V1 to V2. Red-colored state (V1, V4-V7) indicate that inhibition from the states can destabilize the system and possibly cause oscillation. Inhibition from the blue-colored state never induces oscillation.

TOP

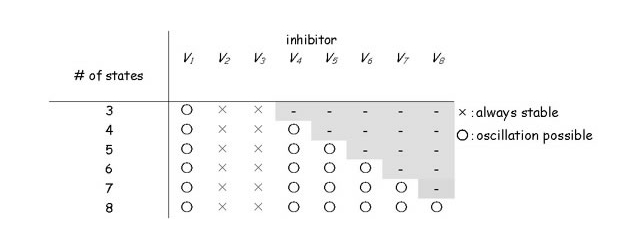
Table 1.

Summary of the results of the general state transition model with conservation of molecules. The system could oscillate when the inhibiting state is more than two steps ahead of the inhibited reaction (from V1 to V2). If the inhibiting state is less than three steps ahead of the reaction, the system is always stable. The necessary distance between the inhibiting state and reactant state does not depend on the system size.

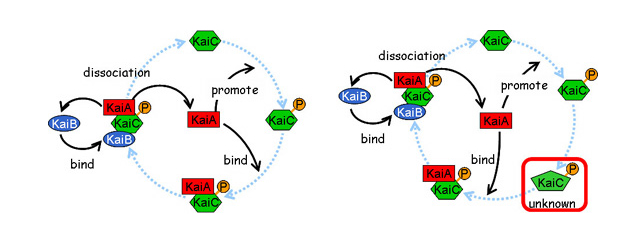
Figure 2

Schematic representations of "Basic model" (left) and "Multiple-phosphorelation-state model" (right). The basic model is determined from experimental results. It was proven that the model never shows oscillation. The multiple-phosphorelation-state model was developed based on the mathematical analysis. The model shows clear periodic oscillations. There are at least two different phosphorelated states and the time-delay caused by the transition between the states is essential for generating oscillation.

Based on this result, we predicted that, in addition to the identified states of KaiC, another unknown state must be present between KaiC phosphorylation and the complex formation. By incorporating the unknown state into the previous model, we realized the periodic pattern reminiscent of the KaiC phosphorylation cycle in computer simulation. This result implies that the KaiC-KaiA complex formation requires more than one step of posttranslational modification including phosphorylation or conformational change of KaiC (Takigawa-Imamura, H., Mochizuki, A. (2006) Predicting regulation of the phosphorylation cycle of KaiC clock protein using mathematical analysis. J Biol. Rhythms 21, 405-416.).