Research
Publications
Member
Access
Photo
Link
Japanese
English
| Relativistic Molecular Theory | |||||||||
| Development of the 2-component RESC and the higher-order Douglas-Kroll (DK) Hamiltonians. RESC and third-order DK methods can easily be incorporated into any ab initio and DFT theory, and proved to be efficient and reliable. A highly efficient computational scheme for solving 4-component Dirac-Fock and Dirac-Kohn-Sham equations is also developed. The result of systems included large relativitic effect showed good accuracy can be obtained by the methods. The methods are implemented in a lot of quantum program package. Recently, The relativistic complete active-space second-order perturbation theory (CASPT2) is developed for the four-component relativistic Hamiltonian. The method gives high accuracy of electronic structure for system include heavy atom by combinatation of the four-component relativistic theory and the complete active-space second-order perturbation theory. | |||||||||
| A relativistic scheme by eliminating small components (RESC) | |||||||||
|
A new relativistic theory has been proposed by the elimination of small components of the Dirac equation. It is variationally stable and can easily be incorporated into any electronic structure theory. A computational cost of RESC method does not change that of non-rekatitistic molecular theory. It is an useful method to incorproate RESC method and high level ab-initio method at for system include heavy atom. |
|||||||||
 |
|||||||||
|
|||||||||
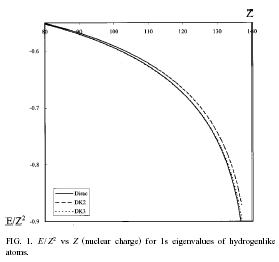
| The higher-order Douglas-Kroll transformation | |||||||||
|
The higher-order Douglas-Kroll (DK) Hamiltonians in an external field are explicitly derived. Application of an exponential-type unitary operator with the 2n+1 rule significantly simplifies the formulations of the high-order DK Hamiltonians. |
|||||||||
  |
|||||||||
| A four-index transformation in Dirac's four-component relativistic theory | |||||||||
|
An efficient integral transformation program based on the four-component spinors resulting from the Dirac-Hartree-Fock (DHF) method is implemented in the REL4D program. By adopting generally contracted spherical harmonic Gaussian-type spinors, the small-component basis functions are almost half as many as the basis expansion with the decoupled scalar spin orbitals. This advantage is exploited to enhance the efficiency in the integral transformation. The present integral transformation program is 4-8 times faster than the pioneering programs of MOLFDIR and DIRAC. |
|||||||||
 |
|||||||||
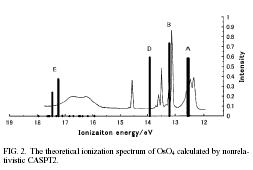
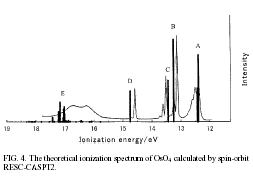
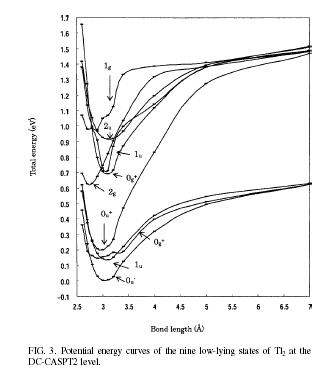
| A relativistic complete active-space second-order perturbation theory (CASPT2) | |||||||||
| The relativistic complete active-space second-order perturbation theory (CASPT2) is developed for the four-component relativistic Hamiltonian. The present method can describe the near-degenerated and dissociated electronic states of molecules involving atoms of heavy elements. For some molecules, the spectroscopic constants of DC-CASPT2 show good agreement with the experimental or previous theoretical spectroscopic constants. The present theory provides accurate descriptions of bonding or dissociation states and of ground and excited states in a well-balanced way. | |||||||||
 |
|||||||||