Research
Publications
Member
Access
Photo
Link
Japanese
English
| A long-range correlation scheme | |||
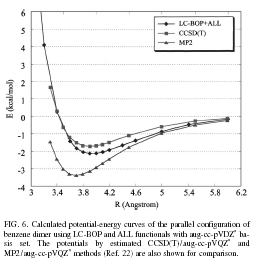
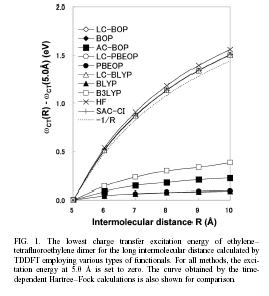
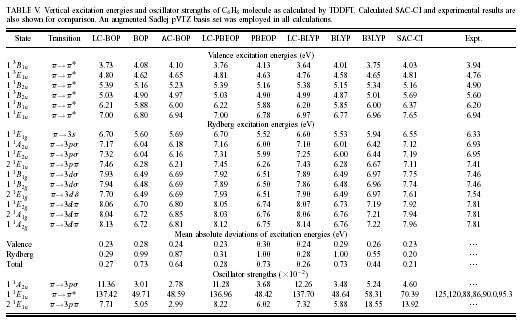
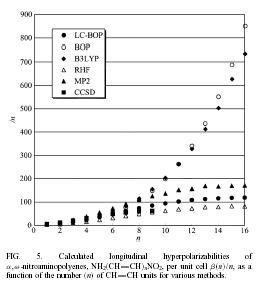
| In the scheme, the standard error function is employed to correct the long-range exchange interaction of the generalized-gradient-approximation (GGA). The LC scheme succeeded to provde accurate potential energy surface of rare-gas dimer and van der waals complexes, pi-atomic interaction of benzene dimer and naphtalene dimer, etc. A long-range corrected (LC)-TDDFT provided accurate Rydberg and charge transfer excitation energy and oscillator strength. LC-TDDFT also improved dipole-moment, polarizability and hyper-polarizability of push-pull conjugated system. | |||
  |
|||
 |
|||
 |
|||
| One-parameter progressive correlation functional (OP correlation functional) |
|||
|
We analyze the Colle-Salvetti correlation functional and propose a new simplified correlation functional called the one-parameter progressive (OP) functional. It contains only one semi-empirical parameter with no adjusted fundamental constant. The functional can be adapted to any kind of exchange functional. Different from generalized gradient approximation type functionals, OP is not derived to obey necessary conditions of the exact correlation functional. However, it is proved that OP satisfies all these conditions if the exchange part is chosen to obey the conditions of the exact exchange functional. Compared to conventional correlation functionals, OP is found to give more accurate correlation energies for atoms, helium through argon, and equivalent chemical properties for G2 set of molecules. |
|||
| Parameter-free exchange functional | |||
|
Conventional generalized-gradient approximations for exchange energy are derived to obey the fundamental conditions of the exact exchange functional. We present a simple analytic exchange functional that does not contain a semiempirical parameter or an adjusted fundamental constant. We show that this functional satisfies several significant and strict fundamental conditions, and gives accurate exchange energies for the atoms, hydrogen through argon, within a margin of error of a few percent. It can be updated for any kind of kinetic-energy density. Surprisingly, the present formalism exactly gives the gradient expansion coefficient for slowly varying density. |
|||
| An efficient state-specific scheme of time-dependent density functional theory (SS-TDDFT) | |||
| A state-specific scheme for time-dependent density functional theory is a method devise for speeding up TDDFT calculations by screening transitions that contribute to a specific excitation. SS-TDDFT accurately reproduced the excitation energies of standard TDDFT while drastically reducing thte rank of the TDDFT responce matrix without loss of accuracy. | |||
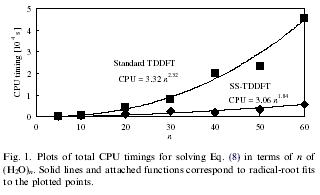 |
|||