Quantum effects melt the spin ice: the spontaneous Hall effect and the time-reversal symmetry breaking without magnetic dipole order

Our recent research in collaboration with University of Tokyo group uncovers the time-reversal symmetry breaking without magnetic dipole order in the frustrated magnet Pr2Ir2O7 [1], suggesting a chiral spin liquid as a result of a melting of spin ice. There have also been accumulated evidences supporting the melting of spin ice accompanied by the quantum nature. How does the spin ice melt? A theoretical scenario has been proposed [2].

Download PDF

日本語版 [Japanese version]

References:

1. Yo Machida, Satoru Nakatsuji, Shigeki Onoda, Takashi Tayama, & Toshiro Sakakibara,

“Time-reversal symmetry breaking and spontaneous Hall effect without magnetic dipole order”,

Nature advanced online publication, 9 December 2009.

2. Shigeki Onoda & Yoichi Tanaka,

“Quantum melting of spin ice into spin smectic with cooperative quadrupole and chirality”,

preprint (ArXiv:0907.2536).

A novel chiral spin state spontaneously breaking the time-reversal symmetry but not forming any magnetic order has been discovered in a metallic magnet through the emergence of the Hall resistivity at zero magnetic field.

The solid state is dominantly determined by the behaviors of a macroscopic number of electrons. Usually, the electronic state in the thermal equilibrium has the time-reversal symmetry. Namely, the state obtained by reversing the motion of all the electrons shows exactly the same physical properties as the original. However, it is known that in some cases, this time-reversal symmetry is broken spontaneously. The typical examples include ferromagnets, where the electronic spin angular momentum and/or orbital angular momentum is imbalanced, producing the magnetization characteristic of the permanent magnet. In principle, the time-reversal symmetry breaking is not restricted to such cases where a magnetic order appears. Even without the observable macroscopic magnetization, the broken time-reversal symmetry on a macroscopic scale could be probed, if the spin chirality, which distinguishes the handedness in which the spins change their directions in space, appears on a macroscopic scale. Cooling a metallic magnetic oxcide containing the praseodymium and the iridium down to extremely low temperatures, we have discovered through the Hall resistivity measurement at zero applied magnetic field a novel thermodynamic phase of matter that shows the spontaneously broken time-reversal symmetry in the absence of magnetic order. This research result is published in Nature Advanced Online Publication on 9 December 2009.

Broken time-reversal symmetry on a macroscopic scale and anomalous Hall effect

Possible scenarios of the spontaneous breaking of the time-reversal symmetry without magnetic order have been investigated intensively and extensively from both theoretical and experimental viewpoints, mainly in the studies of the mechanism and the background of high-temperature cuprate superconductivity. An exotic possibility has been proposed that main roles in forming an order are played by not the spins themselves but the spin chirality of electrons because of strong quantum fluctuations of a macroscopic number of interacting electrons. However, its emergence has not been established yet from both theoretical and experimental viewpoints.

Anomalous Hall effect

One of the most important probes of the broken time-reversal symmetry on a macroscopic scale is provided through the anomalous Hall effect. In metals and semiconductors, the application of electric current I in the perpendicular direction to the applied magnetic field B produces a voltage drop V_H in the direction perpendicular to both the applied magnetic field and electric current. This is the so-called Hall effect, one of the most fundamental electron transport phenomena in solids, and also has significant importance in application. On the other hand, in metallic ferromagnets, a macroscopic magnetization appears through an alignment of electronic spin and/or orbital angular momentum. This magnetization plays a role of the time-reversal symmetry-breaking field as the applied magnetic field does: it breaks the time-reversal symmetry on a macroscopic scale, producing the Hall resistivity (Fig.1A). This is a phenomenon called the anomalous Hall effect. (A recent comprehensive review article on the anomalous Hall effect from both theoretical and experimental viewpoints is being published in a US journal “Reviews of Modern Physics”). A similar phenomenon is also caused by the spin chirality. However, the source of the previously reported Hall effect is restricted to the applied magnetic field and/or a macroscopic magnetization associated with magnetic order. Namely, the spontaneously broken time-reversal symmetry on a macroscopic scale in magnets has been observed only when a certain magnetic order appears with the associated macroscopic magnetization.

Spontaneous Hall effect without magnetic dipole order

We have discovered for the first time in the world a novel state which spontaneously produces the Hall effect at zero magnetic field without any alignment order of electronic spins (Fig.1 B). It has been found in a compound Pr₂Ir₂O₇, which is categorized into magnets having a geometrical frustration, or so-called frustrated magnets. This material contains the praseodymium (Pr) element which plays dominant roles in the nontrivial magnetism of the material. Because of the geometrical frustration, the magnetic moments of Pr³⁺ ions do not form a conventional order even at low temperatures. Instead, it shows a freezing behavior into a glass state at absolute temperature T_f = 0.3 K (Kelvin）. Through detailed measurements of the Hall resistivity and the magnetization, we have detected the spontaneous emergence of the finite Hall conductivity in the temperature range below T_H = 1.5 K above the freezing temperature T_f = 0.3 K where the Pr magnetic moments do not show either magnetic order or freezing behavior (Fig.2).

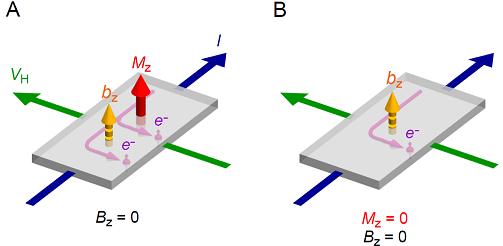
Fig.１ A) The anomalous Hall effect in ferromagnets. The spontaneous magnetization bears a fictitious internal magnetic field b through the relativistic spin-orbit interaction, bending the electronic motion in the direction perpendicular to the applied electric current. B) The Hall effect without magnetic order. Even at zero magnetic field (B = 0), certain states that do not have the spontaneous spin magnetization can show the Hall effect spontaneously. In this case, the fictitious internal magnetic field b, which is a source of bending the electron motion, can be produced by the order of the spin chirality. Since the Hall effect has appeared in our observation spontaneously without both applied magnetic field and spontaneous spin magnetization, the ordering of the spin chirality is naturally considered as a candidate to the origin of the spontaneous Hall effect.

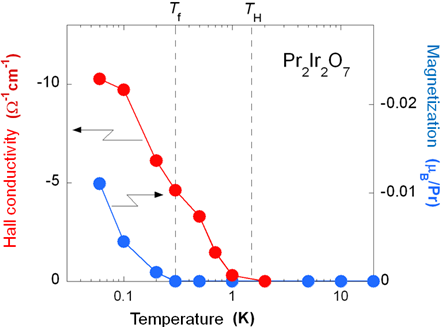
Fig.2　The remnant anomalous Hall conductivity and magnetization measured at zero applied magnetic field as functions of temperature, after the magnetization process up to 7 T (tesla). The remnant anomalous Hall conductivity emerges below an onset temperature T_H ~ 1.5 K well above the spin-freezing temperature T_f ~ 0.3 K. The finite remnant magnetization appears below T_f where the spins look partially frozen.

Quantum melting of spin ice

Then a question arises. Why does such “time-reversal symmetry breaking without magnetic order” emerge? In our recent work described in a preprint, we have made the following key observations common in pyrochlore-lattice magnets Pr₂M₂O₇ (M = Ir, Sn, Zr), derived their effective quantum model, and carried out theoretical analyses. Then, it is found that geometrical frustration of magnetic interactions, which has an analogy in a freezing phenomenon of a water to form an ice, and the quantum nature of electrons play crucial roles.

Geometrical frustration in water ice and spin ice

In an ice into which the water comprising H₂O molecules crystallizes, H⁺ ions are displaced from the vertices of the pyrochlore lattice structure (Fig.3A). Because of hydrogen bonding, the displacements are allowed only in either direction of the O^2- ions located at the centers of the two tetrahedrons sharing this vertex. Namely, if one looks at one tetrahedron, two of the four H⁺ ions are displaced inwards, while the other two are displaced outwards (Fig.3B). Thus, for each O^2- ion, there exist six different ways of choosing two H⁺ ions to form the hydrogen bonding. In the crystal consisting of a macroscopic number of ions, this leaves a macroscopic number of ways.

The geometrical frustration as found in the water ice has also been observed in pyrochlore-lattice magnets R₂Ti₂O₇ (R =Dy, Ho), which has been called a spin ice.

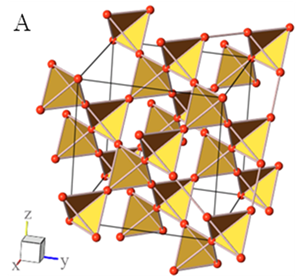
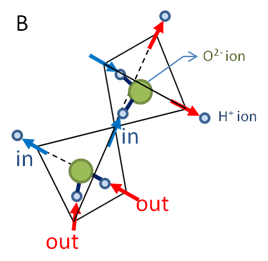
Fig.3: A) Pyrochlore-lattice structure. Red symbols on the vertices of the tetrahedral network represent the basic positions of H⁺ ions in a water ice and the positions of Pr³⁺ ions in Pr₂M₂O₇. B) “2-in, 2-out” tetrahedral configurations. Two H⁺ ions in the case of a water ice and the magnetic moments (spins) of two Pr ions in the case of spin ice point inwards to the center of the tetrahedron, while the other two point outwards.

Quantum effects

A series of pyrochlore-lattice magnets containing Pr³⁺ ions, Pr₂M₂O₇ (M =Ir, Sn, Zr), can be understood as a sort of spin-ice systems but having appreciable quantum fluctuations of magnetic moments. As in classical spin-ice systems R₂Ti₂O₇ (R = Dy, Ho), the directions of magnetic moments of Pr³⁺ ions are severely restricted and they can point either inwards (“in”) to or outwards (“out”) from the center of the tetrahedron (non-Kramers magnetic doublet), which can be described in terms of the so-called Ising spins. In particular, experiments on single crystalline samples of Pr₂Ir₂O₇ show a metamagnetic transition at low temperatures under the applied magnetic field along the [111] direction (Fig.4). This phenomenon should be observed if and only if “2-in, 2-out” tetrahedral configuration is favored at low magnetic field. In this case, one of the four spins always points to the unfavorable direction under the magnetic field applied along the [111] direction. It is flipped to form a “3-in, 1-out” or “1-in, 3-out” configuration when the magnetic field strength exceeds a threshold value comparable to the effective coupling between the spins. This indicates that each tetrahedron is mainly in a “2-in, 2-out” configuration (Fig.3B), and that this spin-ice rule is satisfied in a certain length/time scale. From the value of the magnetic field where the metamagnetic transition has been observed, an effective ferromagnetic coupling has been estimated to be 1.4 K (~ 1.6 meV). These materials do not show a diverging behavior of the magnetic susceptibility unlike the classical spin-ice systems. Because the magnitude of the Pr³⁺ magnetic moment is 1/4 ~ 1/3 of that of the Dy moment, the magnetic dipole-dipole interaction, which is a driving source of the spin-ice behaviors, is of the order of 0.1 K, an order of magnitude smaller. Therefore, a quantum-mechanical superexchange interaction is anticipated to be a dominant interaction between the moments. Actually, neutron-scattering experiments on Pr₂Sn₂O₇ have reported that there appears no magnetic Bragg peak even at the lowest temperature and that the inelastic scattering spectra have a rather broad peak up to 0.2 meV, which is comparable to the effective coupling mentioned above, in an otherwise classical spin-ice behavior. This indicates much stronger quantum fluctuations of the magnetic moments than in the classical spin ice. It suggests an intriguing possibility that the geometrical frustration and the quantum fluctuation cooperatively suppress an conventional magnetic order, and realize a chiral spin liquid where the time-reversal symmetry is broken on a macroscopic scale by the order in the spin chirality, a higher degrees of freedom associated with the spins. Then, we demonstrate theoretically that under the constraints of the spin-ice rule and the zero spin magnetization, it is possible to make a chiral spin structure that produces a finite Hall effect at zero applied magnetic field.

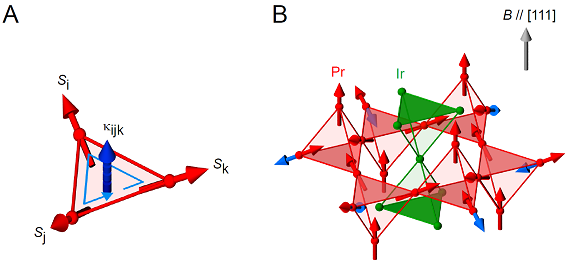
Fig.4 A) The scalar spin chirality k_ijk = S_i・S_j×S_k is defined using three nearby spins in a noncoplanar configuration. B) Crystal structure of Pr₂Ir₂O₇. Both of Pr (red) and Ir (green) atoms form the pyrochlore lattice. Each Pr³⁺ magnetic moment can be described as an Ising spin which points either inwards to or outwards from the center of the tetrahedron. It is most likely that blue arrows indicate the spin directions stable at zero magnetic field, forming “2-in, 2-out” spin-ice configurations together with the red arrows at the other Pr³⁺ sites, and that they are flipped to the red arrows at a metamagnetic transition under the applied magnetic field along the [111] direction. Under the applied field along the [100] and [110] directions, a metamagnetic transition was not observed.

Spin smectic liquid crystal and chirality ice

Now we have recognized theoretically that this state to which the spin ice quantum-mechanically melts shows an analogy to liquid crystals. There are various categories of liquid crystals depending on the way of directional and positional alignments of nonpolar molecules. In particular, that forming a directional order is referred to as a nematic liquid crystal. A prototype of nematic liquid crystals that are optically active because of the helical directional alignments is called a cholesteric liquid crystal. A nematic liquid crystal also showing the positional order is called a smectic liquid crystal. Our recent theoretical studies have uncovered that the spin ice quantum-mechanically melts to a spin analog of the smectic liquid crystal.

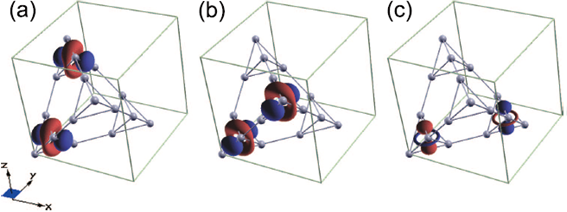
Fig.5 The figures show how the sum of the four magnetic moments (spins) in each tetrahedron is inclined to align each other for nearby tetrahedron pairs. Red and blue regions represent those favorable and unfavorable directions for the sum of the four spins to point. The favorable direction depends on the spatial direction of the two tetrahedrons, but on average, all the spins have a favorable direction of the +z and –z. This results in a compression of the crystal in the z direction.

It has also been found that the quantum state of each tetrahedral unit can be labeled by the left-handed or right-handed chirality. Then, in the quantum melted spin-ice state, the chirality of a tetrahedron is inclined to have an opposite sign between the two tetrahedrons shown in Fig.5. Here, the geometrical frustration found in the freezing behavior of the water appears for the chirality degrees of freedom. This raises a further exotic scenario: a chirality ice which breaks the time-reversal symmetry on a macroscopic scale might be realized as the freezing of the chirality.

The research achievements described here have been produced in Japan. Further theoretical and experimental studies are currently being performed and planned, aiming at a full understanding on the spin liquid with the spontaneously broken time-reversal symmetry and in the quest to a novel state of matter.

The content of this article has been done in collaboration with Y. Machida (Tokyo Institute of Technology, Research Associate), S. Nakatsuji (Institute for Solid State Physics, Univ. of Tokyo, Associate Professor), T. Tayama (Univ. Toyama, Associate Professor), T. Sakakibara (Institute for Solid State Physics, Univ. of Tokyo, Professor), and Y. Tanaka (Condensed Matter Theory Lab., RIKEN, Research Fellow).

References

1. Yo Machida, Satoru Nakatsuji, Shigeki Onoda, Takashi Tayama, & Toshiro Sakakibara, “Broken Time-reversal symmetry and spontaneous Hall effect without magnetic dipole order”, Nature advanced online publication, 9 December 2009.

2. Shigeki Onoda & Yoichi Tanaka, “Quantum melting of spin ice into spin smectic with cooperative quadrupole and chirality”, preprint (ArXiv:0907.2536).

3. H. D. Zhou, C. R. Wiebe, J. A. Janik, L. Balicas, Y. J. Yo, Y. Qiu, J. R. D. Copley, & J. S. Gardner, “Dynamic Spin Ice: Pr₂Sn₂O₇”, Physical Review Letters 101, 227204 (2008).

4. K. Matsuhira, Y. Hinatsu, K. Tenya, H. Amitsuka, & T. Sakakibara, “Low-temperature magnetic properties of pyrochlore stannates”, J. Phys. Soc. Jpn. 71, 1576 (2002).

5. K. Matsuhira, C. Sekine, C. Paulsen, M. Wakeshima, Y.Hinatsu, T. Kitazawa, Y. Kiuchi, Z. Hiroi, & S. Takagi, “Spin freezing in the pyrochlore antiferromagnet Pr₂Zr₂O₇”, J. Phys.: Conference Series 145, 012031 (2009).

6. Naoto Nagaosa, Jairo Sinova, Shigeki Onoda, Allan H. MacDonald, and N. P. Ong, “Anomalous Hall effect”, Reviews of Modern Physics, in press (ArXiv:00904.4154).

7. S. T. Bramwell, “Ferroelectric ice”, Nature (London) 397, 212 (1999); A. P. Ramirez et al., Nature (London) 399, 333 (1999); S. T. Bramwell & M. J. P. Gingras, “Spin ice state in frustrated magnetic pyrochlore materials”, Science 294, 1495 (2001).

Footnotes

（Footnote1）Time-reversal symmetry:

This is one of the most fundamental symmetry in physics under the equilibrium, satisfied if a quantum state shows exactly the same physical properties under the time-reversal operation that also reverse all the motions of particles and waves of interest and thus inverts their wavevectors and angular momenta.

（Footnote2）Magnet. Magnetic order. Ferromagnet:

Magnet is a substance that contains a macroscopic number of microscopic magnetic moments associated with the spin angular momentum, i.e, rotational motion, of electrons. Usually, these electronic spins form a magnetic order in a certain spatial pattern. They are classified into several subclasses; ferromagents (like iron, cobalt, and nickel) having a macroscopic magnetization, antiferromagents where the magnetization is cancelled out within the material, paramagnets that do not show any magnetic order, and so on.

（Footnote 3）Spin chirality:

Three nearby electronic spins, each of which has a directional degree of freedom, may form a noncoplanar structure in materials. Then, the solid angle subtended by these three spins, with the positive or negative sign, depending on whether they form a left-handed or right-handed, is referred to as the spin chirality (Fig.2A). This distinguishes the handedness in the spin space, irrespective of that in the crystal structure.

（Footnote 4）Geometrical frustration:

When the electronic spin located at each vertex of a triangle can point either upwards or downwards and any pair of neighboring spins is forced to align antiferromagnetically, namely, in an anti-parallel configuration (“up, down”), there is no way to achieve these constraints at the same time; one of three pairs has a ferromagnetic configuration (“up, up” or “down, down”). Then, the spins feel “frustration” that originates from the geometry of the lattice structure.

（Footnote 5）High-temperature cuprate superconductivity

The superconductivity accompanied by the zero-resistive state occurs, when charge carriers are chemically doped into mother antiferromagnetic compounds of cuprate ceramics. It is significantly important on scientific grounds as a superconductivity realized in a vicinity of an insulating state. It has also been utilized for application because of its high transition temperature. (The highest transition temperature under pressure amounts to -140 degree in Celsius.)

（Footnote 6）Quantum fluctuation:

In the classical Newtonian physics, the physical observable quantities are always determined at the same time. However, in quantum mechanics describing microscopic physical phenomena, there exist collections of observables that can never be determined simultaneously and completely. For instance, three components of the angular momentum, j_x, j_y, and j_z, are not to be determined at the same time. Then, even upon cooling to the absolute zero temperature, mutually interacting macroscopic number of electrons have directions of their angular momenta fluctuate among various quantum states. In magnets, it is sometimes also called quantum magnetic fluctuations.

（Footnote 7）Spin liquid, chiral spin liquid:

The spin liquid is a system where each electronic spin confined to the magnetic ion site does not have a fixed direction to point and fluctuates both spatially and dynamically. In particular, the spin liquid with the broken time-reversal symmetry on a macroscopic scale is referred to as a chiral spin liquid.

Links

Press release (in Japanese)

Related article in Nakatsuji Group, Institute for Solid State Physics, University of Tokyo

RIKEN homepage

Shigeki Onoda’ｓ homepage

Top