東京大学 先端科学技術研究センター 鈴木研究室 大竹研究室
鈴木・大竹研セミナー
Alexander Belyaev先生 講演会
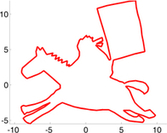
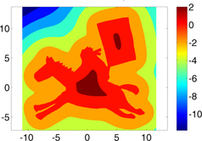
日本でもCG/CAD研究でご活躍された経験をお持ちのAlexander Belyaev先生(Heriot-Watt大学、イギリス)による講演会を下記の様に開催致します。どなたでも聴講出来ますので、お気軽にご参加ください。
講師: Alexander Belyaev (Heriot-Watt大学, UK)
日時: 2013年3月12日(火):14:00-15:00
場所: 東京大学 本郷キャンパス 工学部14号館7階 713会議室
講演言語: 英語
講演タイトル: PDE-based Methods for Smooth Distance Function Approximations
講演要旨:
-
Signed and unsigned distance functions and their smooth approximations are widely used in shape and image analysis, structural mechanics, robotics, biomedical simulations, and many other areas. In this talk, I demonstrate how methods based on Partial Differential Equations (PDE) can be employed for constructing smooth distance function approximations. It is well known that the distance function satisfies an eikonal equation, a simple nonlinear PDE. This leads to PDE-based approaches to build smooth distance functions. Two such approaches are considered. The main idea behind the fist one consists of using the so-called Hopf-Cole transformation which yields an approximation of an eikonal equation by a linear diffusion-like equation. The second approach is based on using generalized double-layer potentials. Links between generalized double-layer potentials and generalized barycentric coordinates are studied. Applications of smooth distance functions to structural mechanics and computer graphics problems are discussed.
- 参考文献:
- A. Belyaev, P.-A. Fayolle, and A. Pasko, "Signed Lp-distance fields", CAD, 45(2): 523-528, 2013 (ACM SPM'12).
- K. Crane, C. Weischedel, and M. Wardetzky, "Geodesics in Heat", CoRR, 2012.
- J. Peng, D. Kristjansson, and D. Zorin, "Interactive Modeling of Topologically Complex Geometric Detail", ACM TOG, 23(3):635-643, 2004 (SIGGRAPH'04).
- K. Gurumoorthy, A. Rangarajan, and A. Banerjee, "The Complex Wave Representation of Distance Transforms", Lecture Notes in Computer Science, 6819:413-427, 2011.
- M. Freytag, V. Shapiro, and I. Tsukanov, "Finite element analysis in situ", Finite Elements in Analysis and Design, 47(9):957-972, 2011.
- R. Gasparini, T. Kosta, and I. Tsukanov, "Engineering analysis in imprecise geometric models", Finite Elements in Analysis and Design, 66:96-109, 2013.
距離場・符号付き距離関数とその滑らかな近似は、形状・画像解析、構造力学解析、ロボティクス、生物・医用シミュレーションなど、多数の分野で幅広く用いられています。本講演では、その様な距離関数を偏微分方程式(PDE)を用いて、どの様に近似するかを示します。距離関数は、簡単な非線形PDEであるEikonal方程式を満たす事が知られており、PDEに基づいた計算法群が提案されています。本講演では、Hopf-Cole変換と呼ばれる変換を用いる事でEikonal方程式を線形拡散方程式にて近似する方法、及び二重層ポテンシャル法を一般化する方式の二つのアプローチについて考えます。また、一般化された二重層ポテンシャルと重心座標系の関係を示し、距離関数のコンピュータ・グラフィクス及び構造力学解析への応用を議論します。
(*): Technicalな詳細よりメインのIdeasに焦点を合わせた講演内容となります。
講師略歴:
-
Alexander Belyaev is currently a Reader in Vision, Image & Signal Processing at Heriot-Watt University, Edinburgh, UK. His main research topics are digital geometry
processing, mathematical image analysis, and applied partial differential equations, on which he published more than one hundred articles in international conferences
and journals. Belyaev co-authored several Best Paper Awards-winning papers at international conferences. Some of his works on surface reconstruction from scattered point data, shape feature extraction, and mesh filtering are widely cited and used by students and scholars worldwide. In 2004-2007 Belyaev worked at Max Planck Institute for Informatics where he led a geometric modeling group. Belyaev's previous employments include Visiting Researcher and Associate Professor at the University of Aizu (1993-2004) and Junior Research Fellow at Moscow State University (1989-1993). Belyaev received his PhD on asymptotic analysis of partial differential equations from Moscow State University in 1990.
-
モスクワ州立大(ロシア)にて「偏微分方程式の漸近解析」によりPhDを取得(1990)。 同大Junior Research Fellow (1989-1993)、会津大学研究員・助教授 (1993-2004)、マックスプランク・コンピュータ科学研究所(ドイツ)上級研究員:CG部門形状モデリンググループ長(2004-2007)を経て、現在はHeriot-Watt大学(イギリス)ビジョン・画像・信号処理グループの準教授(Reader)です。
主に、デジタル幾何・形状処理、数学的画像解析、及び偏微分方程式応用の研究にて、多数の国際会議Best論文賞を含む100を越える国際学術論文を執筆されており、特に、点群からの曲面・表面再構成、形状の特徴抽出、及びメッシュのフィルタ処理の研究群は国際的に幅広く引用されています。
お問い合わせ:
(C) 2013 University of Tokyo, Yutaka Ohtake, Japan. All rights reserved.